Chapitre 3 : Structures de données.
Introduction:
Les structures de données en informatique permettent d'organiser et de gérer les informations de manière efficace, adaptée aux besoins spécifiques des applications et des algorithmes.
Elles sont essentielles pour optimiser le stockage et l'accès aux données.

1. Exercice:
class Truc:
def __init__(self):
self.__liste=[]
def ajout(self,objet):
self.__liste.insert(0,objet)
def enleve(self):
return self.__liste.pop()
def nombre_objets(self):
return len(self.__liste)En considérant la classe Truc ci-dessus :
- Comment qualifier l'attribut
.__liste? -
nouvel_objet=Truc() nouvel_objet.ajout(3) nouvel_objet.ajout(2) nouvel_objet.ajout(10) print(nouvel_objet.enleve()) print(nouvel_objet.nombre_objets())Qu'affiche le code suivant?
-
Schématisez sur votre cahier la façon dont se comporte un objet de classe
Truc.Comment appelle-t-on cela dans la vie courante?
2. Structures de données:
En informatique, que cela soit pour les ordinateurs personnels, les smartphones, les serveurs ou tout autre matériel numérique, nos programmes manipulent un ordre considérable de données
Les programmes actuels structurent leurs données dans les algorithmes.
Il y a plusieurs façons de structurer les données au niveau logiciel.
3. Les structures statiques et dynamiques
A copier dans le cahier.
- Une structure de données statique est un ensemble de données dont la taille est fixée lors de la création de la structure.
- Une structure de données dynamique est un ensemble de données dont la taille peut varier après la création de la structure.
4. Exemples:
- Une liste en Python est structure dynamique car on peut ajouter des données même après sa création.
- Un tuple en Python est une structure statique.
5. Structures linéaires et non linéaires.
A copier dans le cahier.
- Une structure de données linéaire est une structure où les données sont placées les unes à la suite des autres. Chaque élément a un seul prédécesseur hormis la première donnée et chaque élément a un seul successeur hormis la dernière donnée.
- Une structure de données non linéaire est une structure de données qui n'est pas linéaire!
6. Exemples:
- Une liste en Python est une structure linéaire.
- Un arbre hiérarchique n'est pas une structure linéaire (en dehors de la liste chainée).
- Un graphe n'est pas une structure linéaire.
- Les listes chainées sont des structures linéaires.
7. Structures indexées et non indexées.
A copier dans le cahier.
- Une structure de données indexées (ou à accès par clef) est une structure où les données sont accessibles immédiatement sans forcément à avoir à parcourir d'autres données.
- Une structure de données non indexée est une structure où l'accès à certaines données se fait en parcourant d'autres données.
8. Exemples:
- Une liste en Python est une structure indexée par des nombres entiers.
- Un arbre hiérarchique basique est une structure qui se lit en parcourant l'arbre.
- Un graphe n'est pas une structure indexée.
9. Les tableaux.
Un tableau est une structure de données linéaire indexée.
Il faut faire attention au contexte pour savoir si c'est une structure statique ou dynamique.
10. Exercice:
Le but est ici de créer une class TableauStatique qui permet de créer un objet qui est de type statique, indexé et linéaire.
On souhaite avoir les caractèristiques suivantes:
- La taille du tableau est fixé à la création à l'aide de
def __init__(self,taille). - A l'initialisation, le tableau est rempli avec des
None. Cela doit être un attribut privé. - On possède l'attribut
taillequi permet de connaitre la taille du tableau. - Un tableau est considéré comme vide s'il n'est rempli que de
None: on aura ainsi la méthodevide(self)qui renvoie un booléen. La méthode renvoieTruesi le tableau est composé que deNoneetFalsesinon. - On possède la méthode
change(self,i,data)qui permet de changer l'élément d'indiceipar le contenu dedata. - On possède la méthode
effacer(self,i)qui permet de remplacer l'élément d'indiceiparNone. - On possède la méthode
connaitre(self,i)qui permet de savoir le contenu de l'élémenti. - On possède la méthode
affiche_tout(self)qui permet de voir tout le contenu du tableau.
11. Exercice:
Creer une fonction tableau_alea(n) qui prend en paramètre un int nommé n et qui retourne un objet TableauStatiquede taille n contenant des nombres entiers générés aléatoirement entre -20 et 20.
12. Les files et les piles.
A copier dans le cahier.
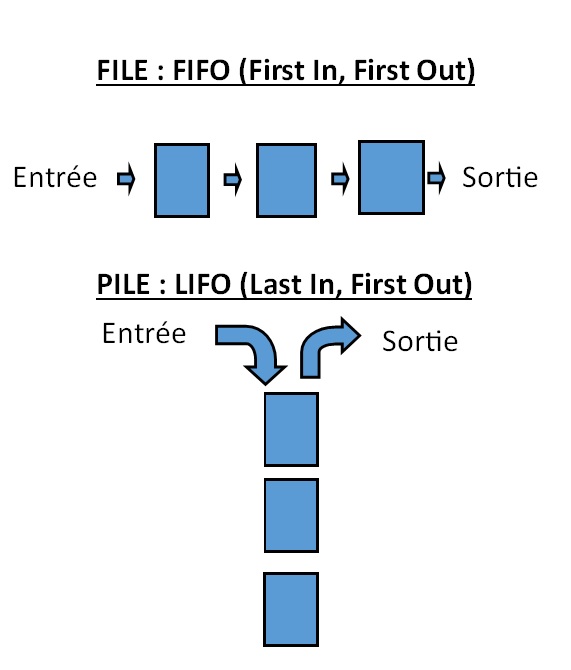
- Une file est une structure de données linéaire, non indexée, qui peut être dynamique et où l'élément que l'on peut sortir est le premier à être rentré.(FIFO : First In, First Out)
- Une pile est une structure de données linéaire, non indexée, qui peut être dynamique et où l'élément que l'on peut sortir est le dernier à être rentré.(LIFO : Last In, First Out)
13. Exemple: La pile dans Python
Par exemple, les piles et les files ne sont pas présentes dans Python.
On peut toutefois créer cet objet avec par exemple la class Pile ci-dessous:
class Pile:
def __init__(self):
self.__tablo = []
def empiler(self, data):
self.__tablo.append(data)
def depiler(self):
return self.__tablo.pop()
def vide(self):
if self.__tablo==[]:
return True
else:
return False
def non_vide(self):
if self.__tablo!=[]:
return True
else:
return False
coucou=Pile()
coucou.push(2)
print(coucou.pop())
print(coucou.vide())14. Exercice:
- Recopier la class
Piledans un fichier python. - Créer une fonction
caracteres_dans_pilequi prend comme paramètre un string et renvoie une pile contenant les caractères de ce string. - Créer une fonction
nb_espacesqui prend comme paramètre une pile contenant des caractères et renvoyant le nombre de fois où le caractère espace apparait sous la forme d'un integer.
15. Exercice:
Créer la classe File contenant les méthodes suivantes:
enfiler(self,data)qui insère un objet dans la filedefiler(self)qui extrait le dernier de la filevide(self)qui teste si la file est videnon_vide(self)qui teste si la file est non vide
16. Exercice:
En utilisant la classe File :
- Creer une fonction
extraire(un_texte)qui prend un string et met chaque caractère dans une file. - Creer une fonction
voyelle(une_file)qui prend une file qui contient des caractères et qui affiche (print) les voyelles présentes. - Creer une fonction
plus_grande(une_file)qui prend une file composée uniquement d'integers et renvoie le plus grand nombre de la file .
17. Exercice : (sujet 8 -2023)
Nous avons l’habitude de noter les expressions arithmétiques avec des parenthèses comme par exemple : \((2 + 3) \times 5\).
Il existe une autre notation utilisée par certaines calculatrices, appelée notation postfixe, qui n’utilise pas de parenthèses. L’expression arithmétique précédente est alors obtenue en saisissant successivement 2, puis 3, puis l’opérateur +, puis 5, et enfin l’opérateur \( \times \). On modélise cette saisie par le tableau [2, 3, '+', 5, '*'].
Autre exemple, la notation postfixe de \( 3 \times 2 + 5\) est modélisée par le tableau :
[3, 2, '*', 5, '+']D’une manière plus générale, la valeur associée à une expression arithmétique en notation postfixe est déterminée à l’aide d’une pile en parcourant l’expression arithmétique de gauche à droite de la façon suivante :
- si l’élément parcouru est un nombre, on le place au sommet de la pile
- si l’élément parcouru est un opérateur, on récupère les deux éléments situés au sommet de la pile et on leur applique l’opérateur. On place alors le résultat au sommet de la pile
- à la fin du parcours, il reste alors un seul élément dans la pile qui est le résultat de l’expression arithmétique.
Dans le cadre de cet exercice, on se limitera aux opérations \( \times \) et \(+\) .
Pour cet exercice, on dispose d’une classe Pile qui implémente les méthodes de base sur la structure de pile.
Compléter le script de la fonction eval_expression qui reçoit en paramètre une liste python représentant la notation postfixe d’une expression arithmétique et qui renvoie sa valeur associée.
class Pile:
"""
Classe definissant une structure de pile.
"""
def __init__(self):
self.contenu = []
def est_vide(self):
"""
Renvoie le booleen True si la pile est vide, False sinon.
"""
return self.contenu == []
def empiler(self, v):
"""
Place l'element v au sommet de la pile
"""
self.contenu.append(v)
def depiler(self):
"""
Retire et renvoie l'element place au sommet de la pile,
si la pile n'est pas vide.
"""
if not self.est_vide():
return self.contenu.pop()
def eval_expression(tab):
p = Pile()
for ... in tab:
if element != '+' ... element != '*':
p.empiler(...)
else:
if element == ...:
resultat = p.depiler() + ...
else:
resultat = ...
p.empiler(...)
return ...Exemples :
>>> eval_expression([2, 3, '+', 5, '*'])
2518. Exercice : (sujet 10 - 2023)
On dispose de chaînes de caractères contenant uniquement des parenthèses ouvrantes et fermantes.
Un parenthésage est correct si :
- le nombre de parenthèses ouvrantes de la chaîne est égal au nombre de parenthèses fermantes.
- en parcourant la chaîne de gauche à droite, le nombre de parenthèses déjà ouvertes doit être, à tout moment, supérieur ou égal au nombre de parenthèses déjà fermées.
Ainsi, "((()())(()))" est un parenthésage correct.
Les parenthésages "())(()" et "(())(()" sont, eux, incorrects.
On dispose de la classe Pile décrite plus bas.
On souhaite programmer une fonction parenthesage qui prend en paramètre une chaîne de caractères ch formée de parenthèses et renvoie True si la chaîne ch est bien parenthésée et False sinon.
Cette fonction utilise une pile et suit le principe suivant : en parcourant la chaîne de gauche à droite, si on trouve une parenthèse ouvrante, on l’empile au sommet de la pile et si on trouve une parenthèse fermante, on dépile (si possible) la parenthèse ouvrante stockée au sommet de la pile.
La chaîne est alors bien parenthésée si, à la fin du parcours, la pile est vide.
Elle est, par contre, mal parenthésée :
- si dans le parcours, on trouve une parenthèse fermante, alors que la pile est vide;
- ou si,à la fin du parcours, la pile n'est pas vide.
Compléter le code ci-dessous :
class Pile:
"""
Classe definissant une pile
"""
def __init__(self):
self.valeurs = []
def est_vide(self):
"""
Renvoie True si la pile est vide, False sinon
"""
return self.valeurs == []
def empiler(self, c):
"""
Place l'element c au sommet de la pile
"""
self.valeurs.append(c)
def depiler(self):
"""
Supprime l'element place au sommet de la pile, a condition qu'elle soit non vide
"""
if self.est_vide() == False:
self.valeurs.pop()
def parenthesage(ch):
"""
Renvoie True si la chaine ch est bien parenthesee et False sinon
"""
p = Pile()
for c in ch:
if c == ...:
p.empiler(c)
elif c == ...:
if p.est_vide():
return ...
else:
...
return p.est_vide()
Exemples :
>>> parenthesage("((()())(()))")
True
>>> parenthesage("())(()")
False
>>> parenthesage("(())(()")
False