Chapitre 19 : Algorithme sur les graphes.

Avant propos :

On fera les exercices dans un nouveau dossier, contenant les fichiers suivants du chapitre graphe :

• france.py qui contient les lignes de code permettant de construire la carte de france.
• structures.py

BFS(graphe, noeud_de_départ):
    file = File()
    file.enfiler(noeud_de_départ)
    Marquer noeud_de_départ comme visité
    Tant que la file n est pas vide:
        noeud_actuel = file.defiler()
        Traiter noeud_actuel
        Pour chaque voisin du noeud_actuel dans le graphe:
            Si il est non visité:
                file.enfiler(voisin)
                Marquer voisin comme visité

2. Exercice :

1. Programmer en Python la fonction parcours_largeur(graphe,noeud_depart) qui prend en paramètres un objet graphe de type GrapheNonOrientePondere et un string noeud_depart. Le traitement du noeud sera simplement l'affichage (print) de la valeur associée à chaque noeud rencontré.
2. Tester cette fonction sur la carte des routes de France avec comme point de départ la ville de Nice.

3. Exercice type bac :

On cherche à lutter contre un virus informatique qui essaie de contourner les protocoles de sécurité en migrant régulièrement vers un autre ordinateur, en choisissant à chaque fois au hasard sa nouvelle cible parmi les ordinateurs accessibles.

On cherche à savoir quels ordinateurs protéger afin de lutter de manière la plus efficace possible avec des ressources limitées.

On considère le réseau informatique suivant, composé de 5 ordinateurs numérotés : 0, 1, 2, 3 et 4.

1. On représente ce réseau informatique par un graphe que l'on stocke sous forme de liste_s de voisins. Compléter la définition de la variable voisins.

   voisins = [ [1, 2, 3, 4],
               [0, 2, 3],
               [0, 1],
               [........],
               [.....]]

On ajoute au réseau actuel un sixième ordinateur, numéroté 5. Cet ordinateur n'est accessible que des ordinateurs numérotés 0 et 2.

2. Dessiner le nouveau graphe sur votre cahier.
3. Modifier la variable voisins afin qu'il corresponde au graphe.

4. Écrire la fonction voisin_alea(voisins, s) qui prend en paramètre un graphe voisins sous forme de listes de voisins et un entier s représentant un sommet et qui renvoie un entier représentant un voisin de s choisi aléatoirement.

   On pourra utiliser la fonction random.randrange(n) qui renvoie un nombre aléatoire entre 0 inclus et n exclus.

On donne la fonction marche_alea suivante :

def marche_alea(voisins, i, n):
    if n==0:
        return i 
    return marche_alea(voisins, voisin_alea(voisins, i), n-1)

5. Justifier que la fonction marche_alea est une fonction récursive.
6. Décrire ce que modélise cette fonction, en rapport avec le contexte de l'exercice.
7. Compléter la fonction simule qui simule n_tests fois le déplacement d'un virus pendant n_pas étapes, démarrant au sommet i, et qui renvoie une liste contenant en position j le nombre de fois que le virus a terminé son parcours au sommet j, divisé par n_tests.

   def simule(voisins , i, n_tests, n_pas) :
       results = [0] * len(voisins)
       .....
           

8. L'appel simule(voisins, 4, 1000, 1000) renvoie la valeur suivante :

   [0.328, 0.195, 0.18, 0.12, 0.059, 0.118].

   Déduire de ce résultat l'ordinateur du réseau qu'il est le plus rentable de protéger.

Au début, on suppose que le virus n'est présent que sur un ordinateur. À chaque étape, il contamine tous ses voisins non déjà contaminés. On cherche à savoir combien de temps prend ce virus pour se propager à tout le réseau.

9. Un graphe voisins représente un réseau, et s représente un sommet de départ.

   Compléter le programme suivant pour déterminer le temps, en étape, que met un virus à se propager à l'intégralité du réseau.

   def nb_etapes_contamination_totale(voisins, s):
       nb_etapes=0
       contamination=[False] * len(voisins) # aucun ordinateur n'est infecté
       contamination[s]=True   # l'ordinateur s devient contaminé
       while ............................... :
   
           #Plusieurs lignes
   
       return nb_etapes
           

   On pourra tester notre code sur ce graphe plus grand :

   

   voisins_nombreux = [
           [1, 2, 3, 4] ,
           [0, 2, 3, 8, 10] ,
           [0, 1, 5, 6] ,
           [0, 1, 9, 12] ,
           [0, 6, 7] ,
           [2, 13, 27] ,
           [2, 4, 7, 14] ,
           [4, 6, 15, 28] ,
           [1, 25] ,
           [3, 26] ,
           [1, 16, 29] ,
           [12, 17] ,
           [3, 11, 18, 30] ,
           [5, 19] ,
           [6, 20] ,
           [7, 21] ,
           [10, 22] ,
           [11, 23] ,
           [12, 24] ,
           [13] ,
           [14] ,
           [15] ,
           [16] ,
           [17, 24] ,
           [18, 23] ,
           [8] ,
           [9] ,
           [5] ,
           [7] ,
           [10] ,
           [12] 
   ]

5. Exercice :

1. Programmer en Python la fonction parcours_profondeur(graphe,noeud_depart) qui prend en paramètres un objet graphe de type GrapheNonOrientePondere et un string noeud_depart. Le traitement du noeud sera simplement l'affichage (print) de la valeur associée à chaque noeud rencontré.
2. Tester cette fonction sur la carte des routes de France avec comme point de départ la ville de Nice.

6. Exercice type bac:

Nous avons représenté sous la forme d’un graphe les liens entre cinq différents sites Web :

La valeur de chaque arête représente le nombre de citations (de liens hypertextes) d’un site vers un autre. Ainsi, le site site4 contient 6 liens hypertextes qui renvoient vers le site site5.

Les sites sont représentés par des objets de la classe Site dont le code est partiellement donné ci-dessous. La complétion de la méthode calcul_popularite fera l’objet d’une question ultérieure.

class Site:
    def __init__(self, nom):
        self.nom = nom
        self.predecesseurs = []
        self.successeurs = []
        self.popularite = 0
        self.couleur = 'blanche'
    
    def calcul_popularite(self):
        pass # sera complété plus tard

Le graphe précédent peut alors être représenté ainsi :

# Description du graphe
s1, s2, s3, s4, s5 = Site('site1'), Site('site2'), Site('site3'), Site('site4'), Site('site5')
s1.successeurs = [(s3,3), (s4,1), (s5,3)]
s2.successeurs = [(s1,4), (s3,5), (s4,2)]
s3.successeurs = [(s5, 3)]
s4.successeurs = [(s1,2), (s5,6)]
s5.successeurs = [(s3,4)]
s1.predecesseurs = [(s2,4), (s4,2)]
s2.predecesseurs = []
s3.predecesseurs = [(s1,3), (s2,5), (s5,4)]
s4.predecesseurs = ...
s5.predecesseurs = ...

1. Sur votre cahier, expliquer la ligne s2.predecesseurs = [].
2. Compléter les deux dernières lignes.
3. Sur votre cahier, expliquer le contenu s2.successeurs[1][1].

Pour mesurer la pertinence d’un site, on commence par lui attribuer un nombre appelé valeur de popularité qui correspond au nombre de fois qu’il est cité dans les autres sites, c’est-à-dire le nombre de liens hypertextes qui renvoient sur lui. Par exemple, la valeur de popularité du site site4 est 3.

4. Quelle est la valeur de la popularité du site 1 ?
5. Compléter le code de la méthode calcul_popularite de la classe Site qui affecte à l’attribut popularite la valeur de popularité correspondante et renvoie cet attribut.

Afin de calculer cette valeur de popularité pour chacun des sites, nous allons faire un parcours dans le graphe de façon à exécuter la méthode calcul_popularite pour chacun des objets.

Voici le code de la fonction qui permet le parcours du graphe :

def parcours_graphe(sommet_depart):
    parcours = []
    sommet_depart.couleur = 'noire'
    liste_s = []
    liste_s.append(sommet_depart)
    while len(liste_s) != 0:
        site = liste_s.pop(0)
        site.calcul_popularite()
        parcours.append(site)
        for successeur in site.successeurs:
            if successeur[0].couleur == 'blanche':
                successeur[0].couleur = 'noire'
                liste_s.append( successeur[0] )
    return parcours

Dans ce parcours, les sites non encore traités sont de couleur 'blanche' (valeur par défaut à la création de l’objet) et ceux qui sont traités de couleur 'noire'.

6. Dans ce parcours, on manipule la liste Python nommée liste_s uniquement à l’aide d’appels de la forme liste_s.append(sommet) et liste_s.pop(0).

   Donner la structure de données correspondant à ces manipulations.

7. Donner le nom de ce parcours de graphe en justifiant.

8. La fonction parcours_graphe renvoie une liste parcours. Indiquer la valeur renvoyée par l’appel de fonction parcours_graphe(s1)

On cherche maintenant le site le plus populaire, celui dont la valeur de popularité est la plus grande.

Voici le code de la fonction qui renvoie le site le plus populaire, elle prend comme argument une liste non vide contenant des instances de la classe Site.

def le_plus_populaire(liste_sites):
    max_popularite = 0
    site_le_plus_populaire=liste_sites[0]
    for site in liste_sites:
        if site.popularite > max_popularite:
            ...
            ...
    return site_le_plus_populaire

9. Compléter la fonction ci-dessus.
10. Expliquer ce que renvoie le_plus_populaire(parcours_graphe(s1)).nom
11. On envisage d’utiliser l’ensemble des fonctions proposées ci-dessus pour rechercher le site le plus populaire parmi un très grand nombre de sites (quelques milliers de sites). Expliquer si ce code est adapté à une telle quantité de sites à traiter. Justifier votre réponse.

8. Exercice:

A faire dans le cahier.

On considère le graphe ci-dessous :

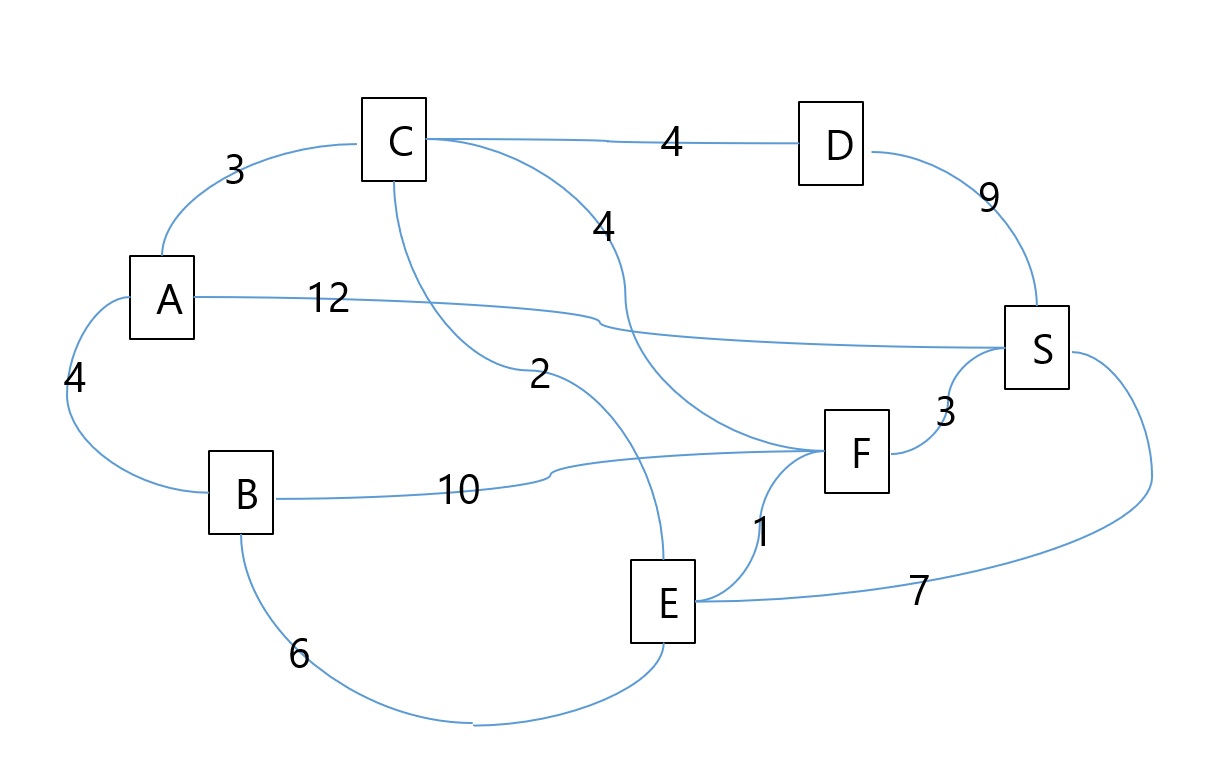
Déterminer à l'aide d'un papier et d'un stylo le plus court chemin entre A et S.

dijkstra(graphe, noeud_de_départ,noeud_arrivee):
    Initialiser une table de distances avec des distances infinies pour tous les noeuds.
    Initialiser une table des noeuds visités en mettant Faux à tous les noeuds.
    Initialiser une table des prédécesseurs vide pour l ensemble des noeuds
    Mettre la distance du noeud_de_départ à 0.
    Mettre le noeud actuel comme étant le noeud de départ.
    Mettre le noeud de départ comme étant visité
    

    Tant que le noeud_arrivee n est pas visité:


        Pour chaque voisin non visité du noeud actuel:
            Calculer la distance temporaire à partir du noeud_de_départ
            Si cette distance temporaire est plus courte que la distance enregistrée dans la table, mettre à jour la distance et le prédecesseur de ce noeud

        Sélectionner le noeud non visité avec la plus petite distance.
        Marquer ce noeud comme visité.
        Mettre ce noeud comme noeud actuel

    Retourner la table des prédécesseurs.

10. Exercice:

1. Compléterl'algorithme de Dijkstra en Python qui prend 3 paramètres : le graphe, le sommet de départ et le sommet d'arrivée. Cette fonction retournera le dictionnaire associant à chaque sommet son prédecesseur afin de former le chemin le plus court entre le noeud le sommet de départ et le sommet d'arrivée.

   import os
   
   os.chdir("u:\\terminaleNSI") # à modifier si nécessaire
   
   import france
   import structures
   import math
   
   routes=france.routes
   
   def dijkstra(graphe,noeud_depart,noeud_arrivee):
   
       #Initialiser une table de distances avec des distances infinies pour tous les noeuds.
       #Initialiser une table des noeuds visités en mettant Faux à tous les noeuds.
       #Initialiser une table des prédécesseurs vide pour l ensemble des noeuds
       dico_distances = {}
       dico_visites = {}
       dico_predecesseurs = {}
   
   
       for noeud in graphe.liste_sommets():
           dico_distances[noeud] = math.inf
           dico_visites[noeud] = False
           dico_predecesseurs[noeud] = ""

2. Tester avec france.routes

3. Ecrire la fonction chemin_le_plus_court(graphe, noeud_depart, noeud_arrivee) qui renvoie la liste des noeuds traversés formant le chemin le plus court entre noeud_depart, noeud_arrivee.

   Par exemple :

   
   >>> chemin_le_plus_court(france.routes, "Nice", "Marseille")
   ["Nice", "Cannes", "Le Luc", "Brignoles", "Aix-en-Provence", "Marseille"]
   

On testera ce programme à l'aide de l'exercice sur les routes du chapitre précédent.

11. Exercice:

Le but de l'exercice est de réfléchir à la recherche de cycle pour les graphes orientés.

Dans la suite de l'exercice, nous appelerons "cycle" tous les chemins dont les points qui le compose sont distincts à l'exception du point de départ et d'arrivée qui sont identiques.

Considérons le code suivant :

def parcours_profondeur(graphe, sommet_depart):
    chemins = []

    def dfs(chemin):
        dernier = chemin[-1]
        if dernier in graphe:
            for voisin in graphe[dernier]:
                deja_dans_chemin = False
                for s in chemin:
                    if s == voisin:
                        deja_dans_chemin = True
                if not deja_dans_chemin:
                    nouveau_chemin = chemin + [voisin]
                    chemins.append(nouveau_chemin)
                    dfs(nouveau_chemin)

    dfs([sommet_depart])
    return chemins


def recherche_de_cycle(graphe, sommet_depart):
    tous_les_chemins = parcours_profondeur(graphe, sommet_depart)
    cycles = []
    for chemin in tous_les_chemins:
        pass
        pass
        pass
        # a completer
    return cycles


# Exemple de graphe orienté pour tester
graphe_test = {
    "A": ["B", "C"],
    "B": ["C", "D"],
    "C": ["A"],
    "D": ["E"],
    "E": ["B"]
}

# Tests
print("Tous les chemins à partir de A :")
for chemin in parcours_profondeur(graphe_test, "A"):
    print(chemin)
'''
print("\nTous les cycles à partir de A :")
for cycle in recherche_de_cycle(graphe_test, "A"):
    print(cycle)

'''

Das

1. Tracer le graphe donné à titre d'exemple dans le code Python sur votre cahier.
2. Y a-t-il des cycles à partir de A? Combien? Lesquels?
3. Que fait la première fonction?
4. Compléter la deuxième fonction afin de chercher des cycles.

12. Exercice :

Ecrire la fonction villes_proches(graphe, ville_depart, distance) qui renvoie une liste de toutes les villes qui sont à un temps inférieur ou égal de ville_depart. 🤯