Chapitre 9 : Diviser pour régner.

2. Exercice : Sujet 9 - 2023

Une utilisation "classique" de "diviser pour régner" est son utilisation sur les listes et avec une récurrence.

Soit tab un tableau non vide d'entiers triés dans l'ordre croissant et n un entier.

La fonction chercher ci-dessous doit renvoyer un indice où la valeur n apparaît dans tab si cette valeur y figure et None sinon.

Les paramètres de la fonction sont :

• tab, le tableau dans lequel s'effectue la recherche
• n, l'entier à chercher dans le tableau
• i, l'indice de début de la partie du tableau où s'effectue la recherche
• j, l'indice de fin de la partie du tableau où s'effectue la recherche

L’algorithme demandé est une recherche dichotomique récursive.

Recopier et compléter le code de la fonction chercher suivante :

def chercher(tab, n, i, j):
    if i < 0 or j > len(tab):
        return None
    elif i > j:
        return None
    m = (i + j) // ...
    if ... < n:
        return chercher(tab, n, ..., ...)
    elif ... > n:
        return chercher(tab, n, ..., ...)
    else:
        return ...

L'exécution du code doit donner :

>>> chercher([1, 5, 6, 6, 9, 12], 7, 0, 10)
>>> chercher([1, 5, 6, 6, 9, 12], 7, 0, 5)
>>> chercher([1, 5, 6, 6, 9, 12], 9, 0, 5)
4
>>> chercher([1, 5, 6, 6, 9, 12], 6, 0, 5)
2

3. Exercice : Sujet 19 - 2023

Écrire une fonction recherche qui prend en paramètres un tableau tab de nombres entiers triés par ordre croissant et un nombre entier n, et qui effectue une recherche dichotomique du nombre entier n dans le tableau non vide tab.

Cette fonction doit renvoyer un indice correspondant au nombre cherché s’il est dans le tableau, -1 sinon.

Exemples :

>>> recherche([2, 3, 4, 5, 6], 5)
3
>>> recherche([2, 3, 4, 6, 7], 5)
-1

5. Exercice : fusion!

Compléter la fonction fusion(liste1,liste2), qui prend comme paramètres deux listes triées et qui renvoie une liste triée composée des élements des deux autres.

def fusion(liste1,liste2):
    '''
    fusion prend deux listes triées et retourne une grand liste triée contenant les éléments des deux autres.
    '''
    final=[]   #liste qui sera retournée
    curseur1=0 #curseur de la liste1
    curseur2=0 #curseur de la liste2
    while ......................................................  : #tant que il reste des éléments non traités dans une des deux listes
        if ...............   : #le plus petit élément est dans la liste 1
            final.append(liste1[curseur1])
            curseur1+=1
        else: #le plus petit élément est celui de la liste 2
            ......................
            ......................

    if ......................... : #il reste des éléments dans la liste 2 à traiter
        for i in range(curseur2,len(liste2)):
            final.append(.......)
    else : #il reste des éléments dans la liste 1 à traiter
        for i in range(curseur1,len(liste1)):
            final.append(.......)
    return final

On pourra tester notre fonction fusion à l'aide des listes suivantes :

listeA=[2,5,7,8,9,11,13,15,19,21,25,29,35,38,39,40,52,69,78,89]
listeB=[3,4,5,7,12,14,15,18,23,30,32,33,34,42,53]

6. Exercice : tri fusion

Compléter la fonction tri_par_fusion(liste) à l'aide de la fonction de l'exercice précédent.

def tri_par_fusion(liste):
    if ............ : # Il y a un élément dans la liste ou moins.
        return liste
    else:
        moitie=......  # indice correspondant au milieu de la liste
        gauche=tri_par_fusion(.............)
        droite=tri_par_fusion(.............)
        return fusion(gauche,droite)

7. Exercice :

A faire dans le cahier.

Ce code a permis de générer les 3 images ci-dessous :

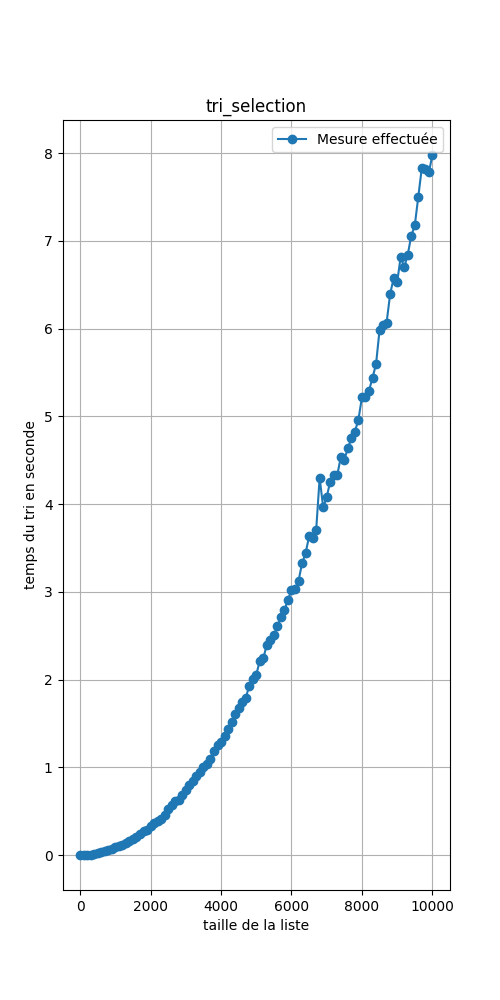
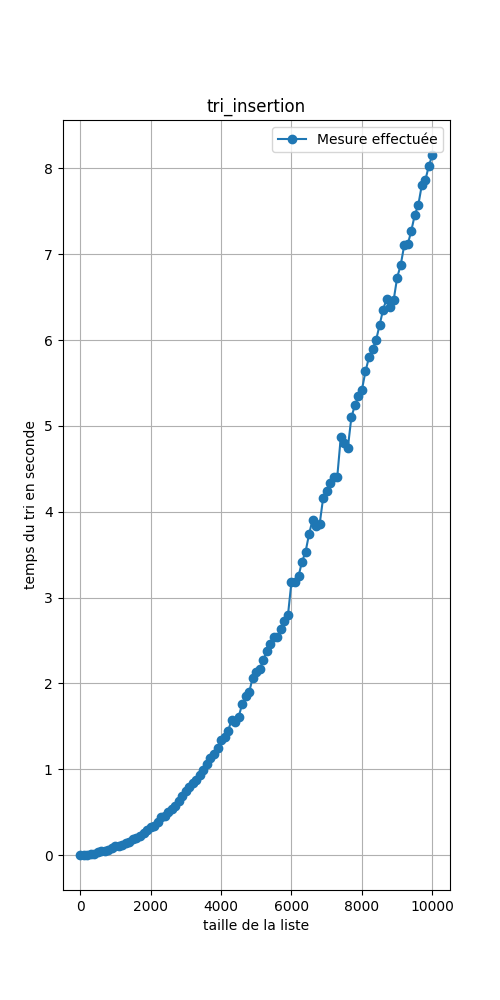
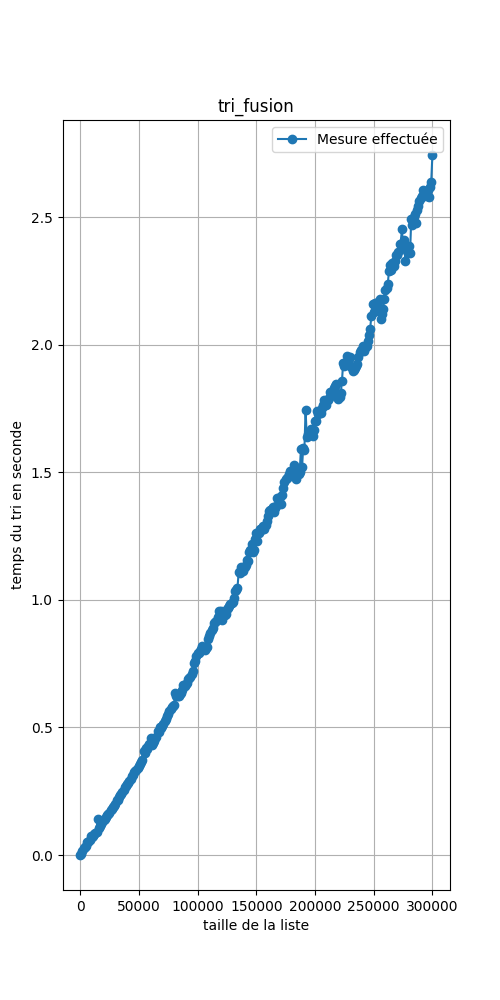
Il peut sembler que les courbes soient similiaires mais :

1. Comparer les performances de chaque tri.
2. A quelle courbe vue en seconde ressemble les deux premières ci-dessus?
3. Quel est l'aspect de la troisième courbe?
4. Dans les deux premières courbes:
   • Prendre deux points de la courbe dont les abscisses sont à peu près le double l'une de l'autre.
   • Calculer une approximation du rapport de ces ordonnées.
5. Dans les deux premières courbes:
   • Prendre deux points de la courbe dont les abscisses sont à peu près le triple l'une de l'autre.
   • Calculer une approximation du rapport de ces ordonnées.
6. Dans les deux premières courbes:
   • Prendre deux points de la courbe dont les abscisses sont à peu près le quadruple l'une de l'autre.
   • Calculer une approximation du rapport de ces ordonnées.
7. Dans la troisième courbe:
   • Prendre deux points de la courbe dont les abscisses sont à peu près le quadruple l'une de l'autre.
   • Calculer une approximation du rapport de ces ordonnées.