Chapitre 1 : Nombres, binaires et octets.

🕐 Historique:

L'histoire des ordinateurs commence au milieu du XXe siècle. Si les premiers ordinateurs ont été réalisés après la Seconde Guerre mondiale, leur conception repose sur le résultat de divers prototypes tels que l'Harvard Mark I et le Z3, machines électromécaniques programmables commencées en 1939, et surtout de deux calculateurs électroniques : le Colossus du service de cryptanalyse britannique en 1943, l'ENIAC en 1945.

Source : wikipedia

1. Introduction:

Actuellement, nos appareils numériques ne savent manipuler que des bits: une succession de 0 et de 1.Cela vient de la conception même de l'électronique actuelle.

On peut alors se poser la question sur la façon dont un appareil numérique manipule d'autres nombres que 0 et 1.

2. Ecriture en base:

A copier dans le cahier.

En mathématique, il n'est pas obligatoire d'écrire un nombre en base 10.

Un nombre écrit sous la forme $a_n a_{n-1} a_ {n-2} ... a_2 a_1 a_0$ en base $b$ signifie qu'il est égal à :

$$ a_n \times b^n + a_{n-1} \times b^{n-1}+ a_ {n-2} \times b^{n-2} + ... +a_2 \times b^2 + a_1 \times b^1 + a_0 $$

3. Notation:

A copier dans le cahier.

Sans mention particulière, si un nombre tel que 314 est écrit, cela sous entend qu'il est écrit en base 10.

La notation $ {a_n a_{n-1} a_ {n-2} ... a_2 a_1 a_0}_b$ sous entend que ce nombre est écrit en base $b$.

Par exemple, $1234_6$ sous entend que ce nombre est écrit en base 6.

4. Exercice:

A faire dans le cahier.

Convertir:

$213_4$ en base 10.
$10_2$ en base 10.
$1001_2$ en base 10.
$10011001_2$ en base 10.
$7$ en base 2.
$20$ en base 2.
$51$ en base 2.
$103$ en base 2.
$1 345$ en base 2.

5. Exercice :

A faire dans le cahier.

Quel est le but du code suivant ?

def un_bit_vers_base_10(binaire): if binaire=="0": return 0 elif binaire=="1": return 1

Tests :

# Tests

Affichage :

Console:

>>>

6. Exercice :

Est programmé ci-dessous une deuxième fonction permettant de transformer un string qui représente un nombre écrit en binaire à deux chiffres et permettant de donner son écriture en base 10.

En suivant cet exemple :

Créer en Python une fonction qui se nomme trois_bits_vers_base_10 et qui prend comme paramètre un string de trois caractères et qui renvoie sa conversion en base 10 sous forme d'un integer.
Créer en Python une fonction qui se nomme quatre_bits_vers_base_10 et qui prend comme paramètre un string de quatre caractères et qui renvoie sa conversion en base 10 sous forme d'un integer.

def un_bit_vers_base_10(binaire): if binaire=="0": return 0 elif binaire=="1": return 1 def deux_bits_vers_base_10(binaire): if binaire=="00": return 0 elif binaire=="01": return 1 elif binaire=="10": return 2 elif binaire=="11": return 3 def trois_bits_vers_base_10(binaire): pass # à compléter def quatre_bits_vers_base_10(binaire): pass # à compléter

Tests :

# Tests

Affichage :

Console:

>>>

7. Exercice :

L'exercice précédent est répétitif et l'on sent que l'on peut faire mieux car nous traitons des cas ressemblant à ceux déjà fait. Par exemple la conversion de '0000' et de '00000' sont similaires.

Si texte est un string, texte[0] désigne le premier caractère et texte[1:] représente tout le string en omettant le premier caractère.

Compléter la fonction ci-dessous qui utilisera quatre_bits_vers_base_10:

def quatre_bits_vers_base_10(binaire): pass # à compléter def cinq_bits_vers_base_10(binaire): if binaire[0]=="0": return ........................... else: return ..... + ..................

Tests :

# Tests

Affichage :

Console:

>>>

8. Exercice :

Les exercices précédents pourraient durer indéfiniment.

Le but est maintenant de compléter la fonction binaire_vers_base_10 qui prend en paramètre un string composé de 0 et de 1 de n'importe quelle taille et qui retourne l'entier convertit en base 10.

def binaire_vers_base_10(binaire): longueur=len(binaire) somme=........ for i in range(longueur): bit=binaire[i] bit=int(......) somme+=......*2**(longueur-i-1) return somme

Tests :

# Tests

Affichage :

Console:

>>>

9. Exercice :

Compléter la fonction base_10_vers_binaire_basique qui prend en paramètre un integer x compris entre 0 et 15 et qui renvoie un string correspondant à son écriture en base 2.

def base_10_vers_binaire_basique(x): if x==0: return "0" elif x==1: return "1" elif ... ... ... ...

Tests :

# Tests

Affichage :

Console:

>>>

10. Algorithme de conversion :

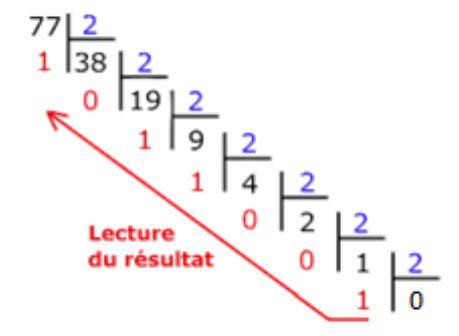
Pour passer d'un nombre écrit en base 10 à son écriture en base deux, on peut utiliser l'algorithme suivant.

Il suffit de faire des divisions par deux successives et de regarder les restes.

11. Exercice:

A faire dans le cahier.

A l'aide de la méthode précédente :

Convertir 12 en base 2.
Convertir 14 en base 2.
Convertir 120 en base 2.

12. Exercice : (issue de l'épreuve pratique de NSI , sujet 38 - 2025 )

On considère la fonction binaire à la page suivante. Cette fonction prend en paramètre un entier positif a en écriture décimale et renvoie son écriture binaire sous la forme d’une chaine de caractères.

Exemples :

>>> binaire(0)
'0'
>>> binaire(77)
'1001101'

def binaire(a): '''convertit un nombre entier a en sa representation binaire sous forme de chaine de caractères.''' if a == 0: return ... bin_a = ... while ... : bin_a = ... + bin_a a = ... return bin_a

Tests :

# Tests

Affichage :

Console:

>>>

13. Hexadecimal

A copier dans le cahier.

En plus de la base de 2, il est indispensable de connaitre pour quelqu'un travaillant dans l'informatique la base 16 (hexadécimal).

Par convention le nombre $10$ est associé à $A_{16}$, 11 à $B_{16}$ et ainsi de suite jusqu'à 15 qui est associé à $F_{16}$.

14. Exercice:

A faire dans le cahier.

Convertir:

$1A_{16}$ en base 10.
$13E_{16}$ en base 10.
$4EA2_{16}$ en base 10.
$101_{16}$ en base 10.
$16$ en base 16.
$35$ en base 16.
$108$ en base 16.
$1 345$ en base 16.

15. Exercice :

Créer une fonction caractere_hexa_vers_base_10 qui prend en paramètre un string d'un seul caractère et qui retourne sa valeur en base 10.

Exemples :

>>> caractere_hexa_vers_base_10('0')
0
>>> caractere_hexa_vers_base_10('9')
9
>>> caractere_hexa_vers_base_10('B')
11

def caractere_hexa_vers_base_10(carac): ...

Tests :

# Tests

Affichage :

Console:

>>>

16. Exercice :

Compléter la fonction ci-dessous. Celle-ci utilisera la fonction caractere_hexa_vers_base_10 de l'exercice précédent.

def caractere_hexa_vers_base_10(carac): # copié-collé ici la fonction de l'exercice précédent def base_16_vers_base_10(hexa): longueur=len(....) somme=.... for i in range(longueur): valeur=.........(hexa[i]) somme+=.....*16**(longueur-i-1) return somme

Tests :

# Tests

Affichage :

Console:

>>>

17. Notation:

A copier dans le cahier.

Un octet (Byte en anglais) est une succession de 8 bits.

18. Exercice:

A faire dans le cahier.

Comment s'écrit le nombre ${0000~0000}_2$ en base 10 ?
Comment s'écrit le nombre ${1111~1111}_2$ en base 10 ?
Combien de nombres entiers distincts peut contenir un octet ?

19. Hexadecimal:

Lorsque qu'un nombre est écrit en base 16, on parle d'écriture en hexadécimale.

20. Conversion de la base 2 à 16 et réciproquement:

A copier dans le cahier.

On peut facilement passer d'une écriture en base 2 en base 16 et réciproquement.

Il suffit de remarquer qu'un nombre écrit en base 2 avec 4 caractères se convertit directement en base 16.

21. Exemple:

A copier dans le cahier.

$ 1011_2 = 11 = B_{16}$
$ 0011_2 = 3 = 3_{16}$

Donc :

$ 1011~0011_2 = B3_{16}$
Mais aussi : $ B3_{16} = 1011~0011_2 $

22. Exercice:

A faire dans le cahier.

Convertir:

$BA_{16}$ en base 2.
$23E_{16}$ en base 2.
$4A2_{16}$ en base 2.
$1111~0101_{2}$ en base 16.
$1100~1011_{2}$ en base 16.
$0110~0011_{2}$ en base 16.
$1000~1001~0110~0011_{2}$ en base 16.

23. Exercice:

A faire dans le cahier.

Poser et effectuer les opérations suivantes:

$3BA_{16} + E6_{16}$.
$BA_{16} - E_{16}$.
$BAE_{16} - AA5_{16}$.
$101~111_{2} + 10~101_{2}$.
$101~000~001_{2} - 10~111_{2}$.

24. Binaire signé et non signé :

Limitons nous aux entiers écrits sur un octet :

Sur un octet, nous pouvons prendre le choix d'encoder soit un entier strictement positif soit un entier relatif c'est à dire pouvant être négatif

Pour cela, nous avons deux possibilités

On peut utiliser la représentation binaire non signé pour les nombres entiers uniquement positifs.
On peut utiliser la représentation binaire signé pour les nombres entiers relatifs.

25. Binaire non signé :

Dans le cas d'un binaire non signé, l'écriture en base 2 d'un nombre et son écriture en binaire correspondent.

Par exemple, le nombre 16 peut être encodé sur un octet : 0001 0000

26. Binaire signé :

A copier dans le cahier.

Dans le cas d'un binaire signé, on utilise la méthode suivante:

Si c'est un entier positif, on utilise son écriture en base 2

Si c'est un entier négatif, on prend l'écriture de son opposé en base 2, puis son complément à 2 (on inverse les 0 et les 1) puis on ajoute 1

27. Exemple:

Essayons de trouver l'écriture du nombre -20 sur un octet.

L'écriture de 20 en base 2 écrit sur un octet est 0001 0100
Son complément à 2 est 1110 1011
On ajoute 1 : 1110 1100

L'écriture de -20 en binaire signé est 1110 1100 sur un octet.

Vérification :

$$ \begin{equation} \begin{aligned} &00010100_2 \\ + &11101100_2 \\ = \color{red}1&\color{green}00000000_2 \end{aligned} \end{equation} $$

28. Exercice:

A faire dans le cahier.

Donner les écritures sur un octet des nombres suivants:

24 en binaire non signé
24 en binaire signé
-38 en binaire signé
-1 en binaire signé
Le nombre associé à l'octet 1100 0001 en binaire non signé.
Le nombre associé à l'octet 1100 0001 en binaire signé.

29. Nombres décimaux et réels:

Un nombre écrit sous la forme $a_n a_{n-1} ... a_ {1} a_ {0},a_ {-1} ... a_{-m}$ en base $2$ signifie qu'il est égal à :

$$ a_n \times 2^{n} + a_{n-1} \times 2^{n-1}+...+ a_ 1 \times 2^1 +a_ 0 \times 2^0 + a_ {-1} \times 2^{-1} +... +a_{-m} \times 2^{-m}$$

30. Exemple:

Essayons de trouver l'écriture en base 10 du nombre $101,011_2$.

$$ \begin{equation} \begin{aligned} \color{red}{101,011_2} &= \color{red}{1} \color{green}{ \times 2^2 +}\color{red}{0} \color{green}{\times 2^1 + }\color{red}{1} \color{green}{\times 2^0 + }\color{red}{0} \color{green}{\times 2^{-1} + }\color{red}{1} \color{green}{\times 2^{-2} + }\color{red}{1} \color{green}{\times 2^{-3}}\\ &= 4+1+\frac{1}{4} + \frac{1}{8} \\ &=4+1+0,25+0,125\\ &= 5,375 \end{aligned} \end{equation} $$

31. De la base 10 à la base 2 pour les nombres décimaux : les problèmes arrivent..

Pour passer de la base 10 à la base 2, nous pouvons utiliser les algorithmes utilisés pour les nombres entiers. Mais parfois les écritures en base 2 comportent une infinité de chiffres après la virgule.

32. Exemples:

Essayons de trouver l'écriture en base 2 du nombre 5,25 :

La plus grande puissance de 2 intervenant est $2^2$.
$$ \begin{equation} \begin{aligned} 5,25 &= 2^2+1,25\\ &= 2^2+2^0 + 0,25\\ &= 2^2+2^0+2^{-2}\\ &= 101,01_2 \end{aligned} \end{equation} $$
Essayons de trouver l'écriture en base 2 du nombre 5,2 :

La plus grande puissance de 2 intervenant est $2^2$.
$$ \begin{equation} \begin{aligned} 5,2 &= 2^2+1,2\\ &= 2^2+2^0 + 0,2\\ &= 2^2+2^0 + 0,125+0,075\\ &= 2^2+2^0+2^{-3}+0,075\\ &= 2^2+2^0+2^{-3}+0,0625+0,0125\\ &= 2^2+2^0+2^{-3}+2^{-4}+0,0125\\ &= 2^2+2^0+2^{-3}+2^{-4}+0.0078125 + 0,0046875\\ &= 2^2+2^0+2^{-3}+2^{-4}+2^{-7} +0,0046875\\ &= 2^2+2^0+2^{-3}+2^{-4}+2^{-7} + 0.00390625 +0.00078125\\ &= 2^2+2^0+2^{-3}+2^{-4}+2^{-7} + 2^{-8 } +0.00078125 \\ &= 2^2+2^0+2^{-3}+2^{-4}+2^{-7} + 2^{-8 } + 0.00048828125 + 0.00029296875 \\ &= 2^2+2^0+2^{-3}+2^{-4}+2^{-7} + 2^{-8 } + 2^{-11} + 0.00029296875 \\ &= 2^2+2^0+2^{-3}+2^{-4}+2^{-7} + 2^{-8 } + 2^{-11} + 0.000244140625 + 0.000048828125 \\ &= 2^2+2^0+2^{-3}+2^{-4}+2^{-7} + 2^{-8 } + 2^{-11} + 2^{-12} + 0.000048828125 \\ &= 2^2+2^0+2^{-3}+2^{-4}+2^{-7} + 2^{-8 } + 2^{-11} + 2^{-12} + 2^{-15}+.............. \\ &=101,0011001100110011001100110011001100110011001100110011........_2 \end{aligned} \end{equation} $$
Pour se persuader du nombre de chiffre après la virgule, on peut s'aider des égalités suivantes:
$$ \begin{equation} \begin{aligned} 0,2&=\frac{2}{10} \\ &=\frac{1}{5} \\ &=\frac{1}{8} + \frac{1}{16} + \frac{1}{80}\\ &= \frac{1}{8} + \frac{1}{16} + \frac{1}{16} \times \frac{1}{5} \\ &= 2^{-3} + 2^{-4} + 2^{-4} \times \color{red}(\frac{1}{5} ) \\ \color{black}&= 2^{-3} + 2^{-4} + 2^{-4} \times \color{red}(2^{-3} + 2^{-4} + 2^{-4} \times \color{green}(\frac{1}{5} ) \color{red}) \\ \color{black}&= 2^{-3} + 2^{-4} + 2^{-7}+ 2^{-8} + 2^{-8} \times \color{green}(\frac{1}{5} ) \color{black} \\ \color{black}&= 2^{-3} + 2^{-4} + 2^{-7}+ 2^{-8} + 2^{-8} \times \color{green}(2^{-3} + 2^{-4} + 2^{-4} \times \color{blue}(\frac{1}{5} ) \color{black}) \\ \color{black}&= 2^{-3} + 2^{-4} + 2^{-7}+ 2^{-8} + 2^{-11} + 2^{-12} + 2^{-12} \times \color{blue}(\frac{1}{5} ) \\ &=... \end{aligned} \end{equation} $$ A chaque étape, il restera toujours la fraction $\frac{1}{5}$

33. Nombres à virgule fixe ou à virgule flottante:

En ce qui concerne les nombres décimaux, en informatique nous pouvons avoir deux approches:

Le nombre de chiffres maximal après la virgule est fixé dès le départ.
Le nombre de chiffres maximal après la virgule n'est en soi pas limité, c'est le nombre de chiffre significatif qui l'est. On parle d'un codage des nombres à virgule flottante.

Chapitre 1 : Nombres, binaires et octets.

🕐 Historique:

1. Introduction:

2. Ecriture en base:

3. Notation:

4. Exercice:

5. Exercice :

6. Exercice :

7. Exercice :

8. Exercice :

9. Exercice :

10. Algorithme de conversion :

11. Exercice:

12. Exercice : (issue de l'épreuve pratique de NSI , sujet 38 - 2025 )

13. Hexadecimal

14. Exercice:

15. Exercice :

16. Exercice :

17. Notation:

18. Exercice:

19. Hexadecimal:

20. Conversion de la base 2 à 16 et réciproquement:

21. Exemple:

22. Exercice:

23. Exercice:

24. Binaire signé et non signé :

25. Binaire non signé :

26. Binaire signé :

27. Exemple:

28. Exercice:

29. Nombres décimaux et réels:

30. Exemple:

31. De la base 10 à la base 2 pour les nombres décimaux : les problèmes arrivent..

32. Exemples:

33. Nombres à virgule fixe ou à virgule flottante:

34. Base 2 vers base 10 :

35. Base 10 vers base 2 :