duranton.net

Introduction :

Le tri par insertion est un autre algorithme de tri qui fonctionne en construisant une liste triée un élément à la fois.

Contrairement au tri par sélection, où on cherche le plus petit élément à chaque étape, le tri par insertion prend chaque élément de la liste non triée et l'insère à sa place correcte dans la partie déjà triée. Ce processus est répété pour tous les éléments.

Le tri par insertion est souvent plus efficace que le tri par sélection pour les petites listes ou les listes déjà partiellement triées, mais il a également une complexité en temps de O(n2)O(n2) dans le pire des cas.

1. Tri par insertion .

A copier dans le cahier.

Le tri par insertion est un algorithme de tri simple qui construit une liste triée un élément à la fois en insérant chaque élément à sa place appropriée dans la partie triée de la liste.

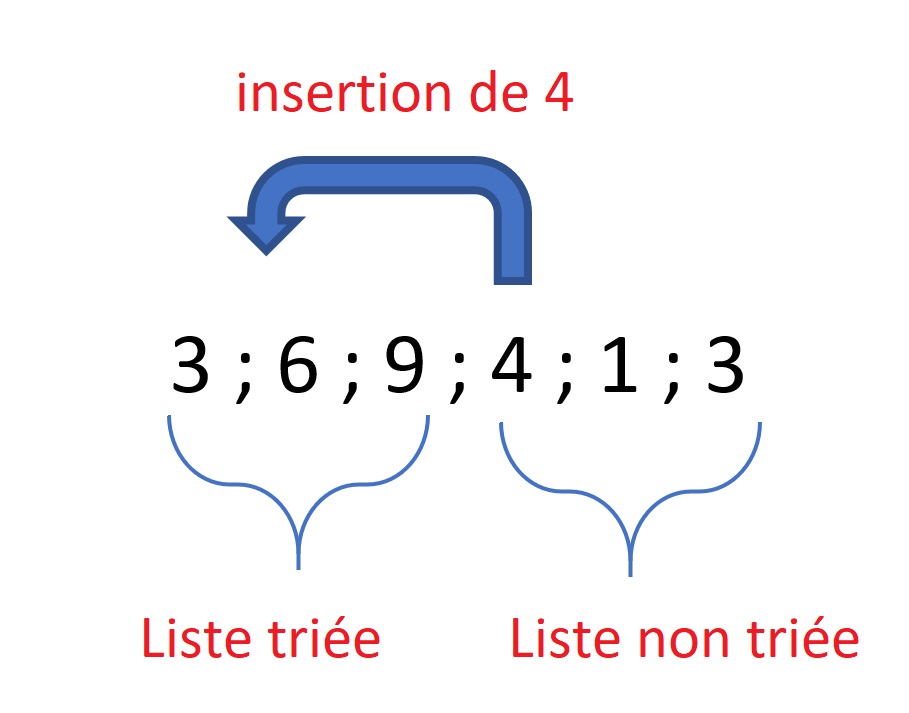
L'algorithme de tri par insertion fonctionne comme suit :

Commencer avec le deuxième élément (l'élément à l'index 1) et le comparer avec le premier élément. Si le deuxième élément est plus petit, les échanger.
Continuer à déplacer l'élément comparé vers la gauche jusqu'à ce qu'il atteigne sa position appropriée parmi les éléments triés précédents.
Répéter les étapes 1 et 2 pour tous les éléments suivants dans la liste non triée.

2. Exercice :

A faire dans le cahier.

A la main :

Trier la liste [42, 17, 9, 87, 23, 56, 34, 71, 5, 91] en mettant une ligne par étape avec un algorithme de tri par insertion.

3. Exercice

Compléter la fonction suivante :

liste = [9, 5, 8, 4, 0, 2, 7, 1, 10, 3, 6]

def tri_insertion(tab):
    n = len(tab)
    for i in range(1, n):
        valeur_insertion = tab[...]
        # la variable j sert a determiner ou placer la valeur a  ranger
        j = ...
        # tant qu'on a pas trouve la place de l'element a inserer
        # on decale les valeurs du tableau vers la droite
        while j > ... and valeur_insertion < tab[...]:
            tab[j] = tab[j-1]
            j = ...
        tab[j] = ...

4. Complexité du tri par insertion.

La complexité d'un tri permet de connaitre "sa lenteur".

Celui du tri par insertion est \(\mathcal{O}\left(n^2\right)\).

Cela signifie que, globalement, si une liste est 2 fois plus longue, il sera 4 fois plus long de la trier. Si la taille d'une liste est multipliée par 10, il sera 100 fois plus long de la trier etc.

5. Exercice