duranton.net

Chapitre 15 : Architecture de Von Neumann.

Introduction:

Nous allons tâcher de comprendre de manière non approfondie la façon dont fonctionne un ordinateur.

1. Le transistor:

Les ordinateurs utilisent des transistors, inventés en 1947. Avant cela, des tubes à vide (plus grands et moins fiables) remplissaient le même rôle, comme dans l’ordinateur Colossus (1943).

Aujourd’hui, les transistors ne sont plus séparés : ils sont gravés par millions dans des circuits intégrés sur des plaques de silicium, ce qui rend les ordinateurs plus compacts et plus fiables.

2. Circuits logiques:

Le transistor est l’élément de base des circuits logiques. Un circuit logique permet de réaliser une opération booléenne. Ces opérations booléennes sont directement liées à l’algèbre de Boole. Un circuit logique prend en entrée un ou des signaux électriques (chaque entrée est dans un état ”haut” (symbolisé par un ”1”) ou à un état ”bas” (symbolisé par un ”0”)) et donne en sortie un ou des signaux électriques (chaque sortie est aussi dans un état ”haut” ou à un état ”bas”). Il existe deux catégories de circuit logique :

Dans la suite nous nous intéresserons principalement aux circuits combinatoires.

3. La porte "non":

Le plus simple des circuits combinatoires est la porte ”NON” qui inverse l’état en entrée : si l’entrée de la porte est dans un état ”bas” alors la sortie sera dans un état ”haut” et vice versa. Si on symbolise l’état ”haut” par un ”1” et l’état ”bas” pour un ”0”.

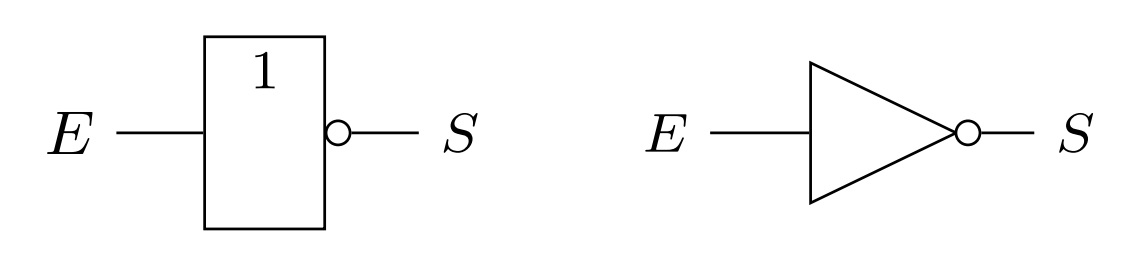
4. Exercice:

A faire dans le cahier.

Etablir la table de vérité de la porte "non".

5. La porte "ou":

La porte "ou" est un circuit combinatoire dont voici le symbole :

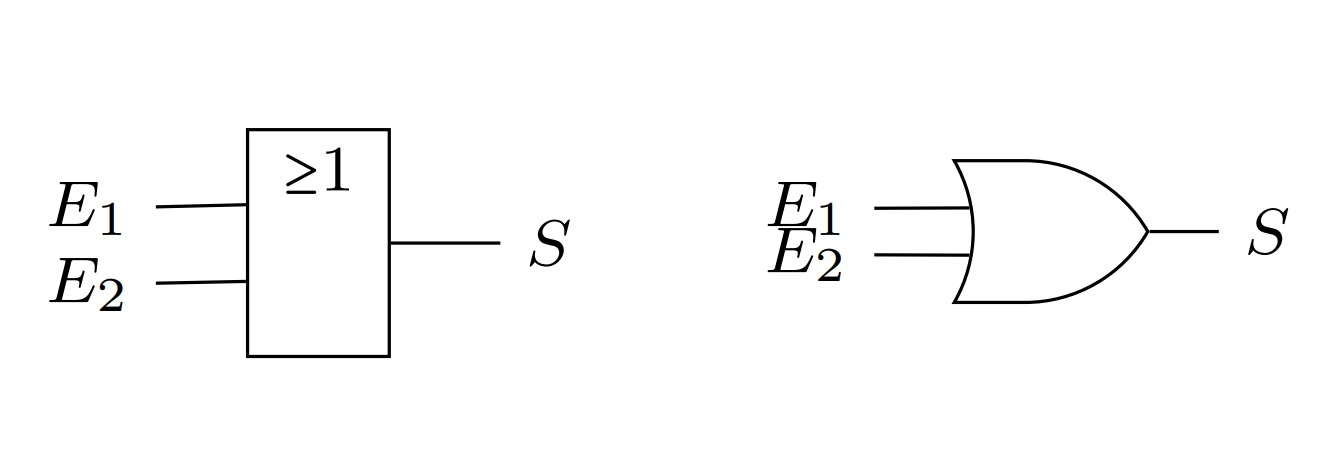
6. Exercice:

A faire dans le cahier.

Etablir la table de vérité de la porte "ou".

7. La porte "et":

La porte "et" est un circuit combinatoire dont voici le symbole :

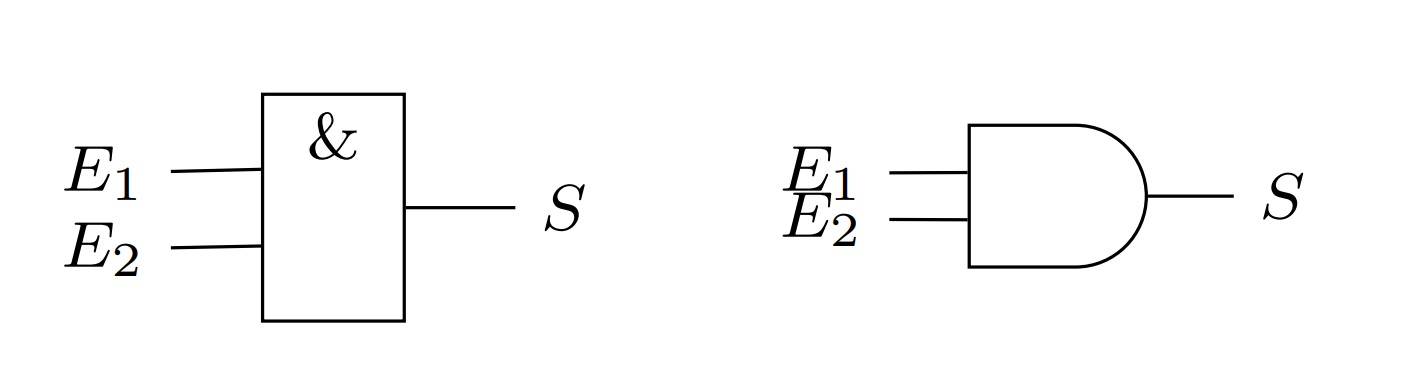
8. Exercice:

A faire dans le cahier.

Etablir la table de vérité de la porte "et".

9. La porte "ou exclusif":

La porte "ou exclusif" aussi appelé "XOR" est un circuit combinatoire dont voici le symbole :

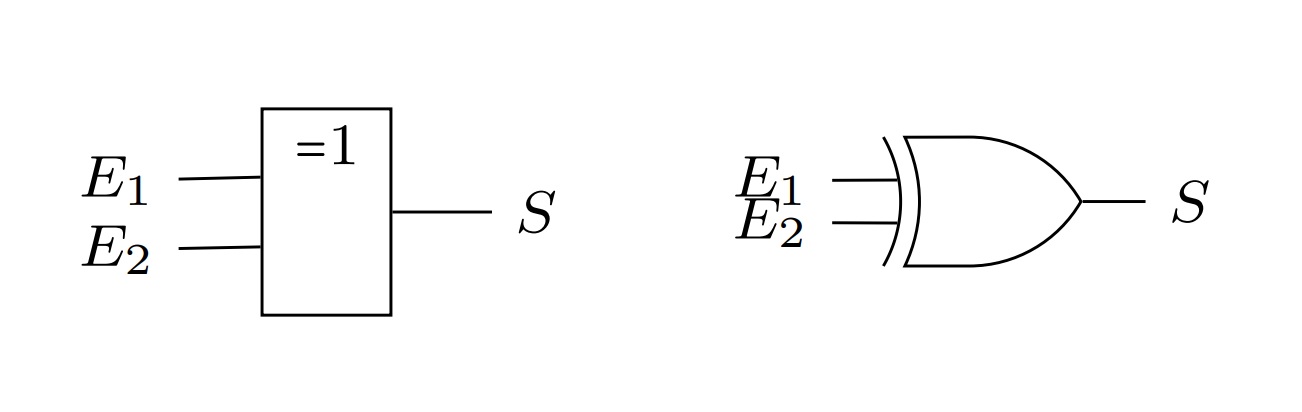
10. Exercice:

A faire dans le cahier.

Etablir la table de vérité de la porte "ou exclusif".

11. Exercice : (sujet 35 - 2023)

L'opérateur « ou exclusif » entre deux bits renvoie 0 si les deux bits sont égaux et 1 s'ils sont différents. Il est symbolisé par le caractère \( \oplus \).

Ainsi :

On représente ici une suite de bits par un tableau contenant des 0 et des 1.

Exemples :

a = [1, 0, 1, 0, 1, 1, 0, 1]
b = [0, 1, 1, 1, 0, 1, 0, 0]
c = [1, 1, 0, 1]
d = [0, 0, 1, 1]

Écrire la fonction ou_exclusif qui prend en paramètres deux tableaux de même longueur et qui renvoie un tableau où l’élément situé à position i est le résultat, par l’opérateur « ou exclusif », des éléments à la position i des tableaux passés en paramètres.

En considérant les quatre exemples ci-dessus, cette fonction donne :

>>> ou_exclusif(a, b)
[1, 1, 0, 1, 1, 0, 0, 1]
>>> ou_exclusif(c, d)
[1, 1, 1, 0]

12. Exercice:

A faire dans le cahier.

On considère le schéma suivant :

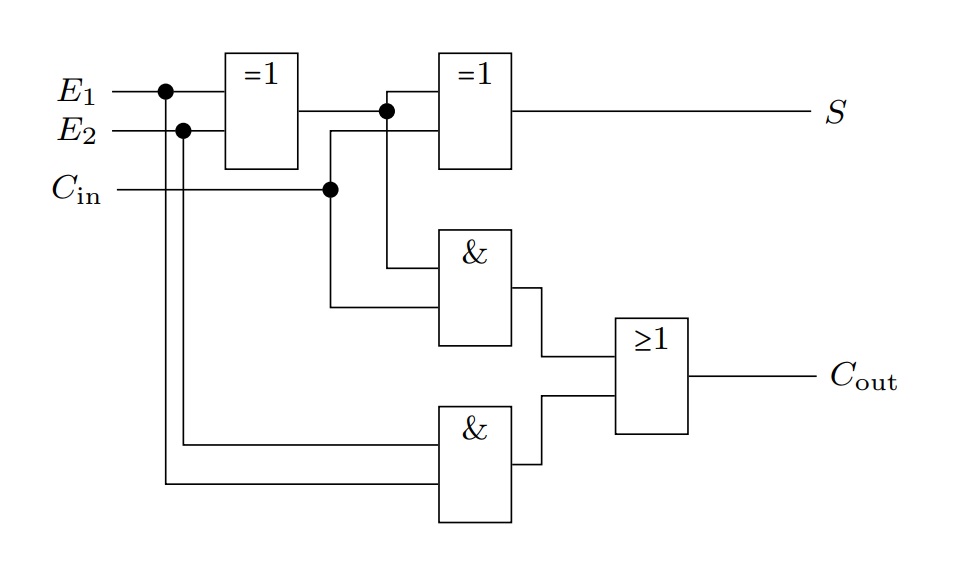
  1. Compléter la table de vérité suivante:

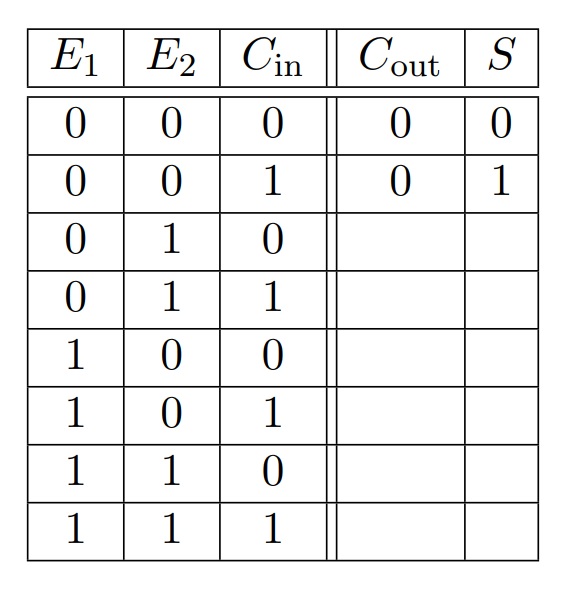
  2. A quoi sert ce circuit selon vous?

13. La mémoire RAM:

La mémoire est un ensemble de cellules, chacune stockant 1 octet et possédant sa propre adresse. On peut lire ou écrire un octet dans n’importe quelle cellule directement. C’est pour cela qu’on parle de RAM (Random Access Memory), car on accède librement à chaque adresse.

Chaque bit est conservé dans un condensateur associé à un transistor : un condensateur chargé représente un “1”, déchargé un “0”. Comme le condensateur doit être alimenté pour garder sa charge, la mémoire est volatile : sans courant, son contenu est perdu.

14. Organisation d'un CPU:

Le CPU exécute les instructions des programmes. Il comprend :

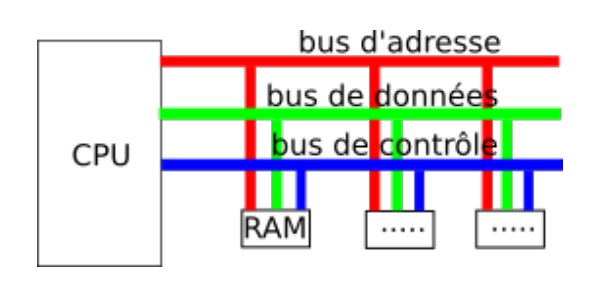
Pour déplacer les données entre la mémoire et le CPU, on utilise le bus :

15. Fonctionnement d'un CPU:

Le processeur exécute un langage machine : un ensemble d’instructions prédéfinies. Chaque instruction comporte :

Programme et données se trouvent tous deux en RAM. Le CPU dispose de registres spéciaux :

Le CPU suit un cycle :

  1. Copier en IR l’instruction à l’adresse IP.
  2. Décoder l’instruction (activer le circuit nécessaire).
  3. L’exécuter (et mettre à jour IP).

Le langage machine est Turing-complet, donc capable d’exécuter tout programme. Dans le modèle de von Neumann, code et données partagent la même mémoire : un même contenu binaire peut servir d’instruction ou de donnée. Certains pirates exploitent cette ambigüité pour exécuter du code malveillant. Les processeurs modernes permettent alors de marquer des zones mémoire comme non-exécutables pour limiter ces attaques.

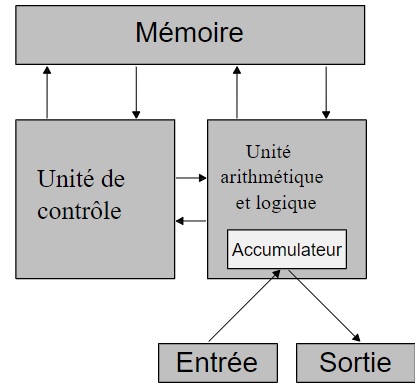
16. Organisation d'un CPU:

Schéma classique d'une architecture de Von Neumann :

17. Qu’est-ce que le langage machine ?

Le langage machine est le niveau le plus bas de programmation, interprété directement par le processeur. Il est composé d’instructions binaires (0 et 1) que le processeur exécute sans traduction supplémentaire. Pour mieux comprendre le langage machine, il est important de voir la différence entre :

Les programmes écrits dans un langage de haut niveau sont traduits (compilés ou interprétés) en instructions compréhensibles par la machine.

18. Les instructions et le codage binaire

Le processeur ne comprend que des suites de bits (0 ou 1), appelées instructions machines. Chaque processeur a son propre jeu d’instructions (son ISA – Instruction Set Architecture).

Dans un système simplifié, on pourrait définir que 4 bits définissent l’opération, et 8 bits définissent l’opérande (la donnée ou l’adresse utilisée par l’opération). Par exemple :

Grâce à ce codage, un programme n’est qu’une suite d’instructions binaires chargées en mémoire. Le processeur les lit, les décode et les exécute.

19. Vers l’assembleur et la programmation de bas niveau

L’assembleur est un langage de plus haut niveau que le langage machine, mais il reste proche du matériel. Chaque instruction en assembleur correspond en général à une instruction machine. Par exemple, au lieu d’écrire 0001 00000010, on écrira ADD 2.

L’assembleur est donc plus lisible pour l’humain, tout en restant très près du fonctionnement réel du processeur. Il existe un assembleur différent pour chaque type de processeur. Apprendre l’assembleur permet de comprendre comment sont organisées les instructions machines, comment sont gérés les registres, etc.

20. Exemple : correspondance assembleur/machine

Voici un petit extrait montrant la correspondance directe :

Assembleur       Binaire
---------------------------
MOV 10           0100 00001010
ADD 2            0001 00000010
SUB 4            0010 00000100
MUL 3            0011 00000011
HLT              1111 00000000

Dans un vrai processeur x86, ARM ou autre, ces codes binaires sont bien plus riches et complexes, mais le principe de base reste similaire : le processeur exécute une suite d'instructions codées en binaire.

21. Exercice

Simulation d’un mini-processeur (MOV, ADD, SUB, MUL, HLT)

Faisons une version extrêmement simplifiée de la façon dont un programme de haut niveau comme Python pourrait être traduit en assembleur et qui pourrait être lui même traduit en langage machine.

Considérons le code suivant : 

x=20
x=x+5
x=x*3
x=x-4
x=x+10
x=x*2
print(x)

L'initialisation x=20se fait à l'aide de la commande MOV 20.

Transformer les lignes de code ci-dessus en instruction assembleur et langage machine à l'aide de l'outil ci-dessous.

Mémoire



    
    

    
Logs d’exécution