Chapitre 9 : Diviser pour régner.
Rappel :
Vous avez vu l'année dernière le tri par insertion et le tri par selection et tous les deux avaient une complexité en \(\mathcal{O}\left(n^2\right)\).

1. Diviser pour régner (divide and conquer) :
A copier dans le cahier.
C’est une méthode de conception d’algorithmes qui consiste à :
- Diviser un problème en sous-problèmes plus petits et de même nature ;
- Résoudre récursivement ces sous-problèmes ;
- Combiner les solutions obtenues pour construire la solution du problème initial.
Des exemples classiques d’algorithmes « diviser pour régner » sont le tri fusion (merge sort), le tri rapide (quick sort) ou encore la recherche dichotomique.
2. Exercice : (sujet 9 - 2025)
On s’intéresse à la recherche dichotomique dans un tableau trié d’entiers.
Compléter la fonction suivante en respectant la spécification.
Exemples :
>>> dichotomie([15, 16, 18, 19, 23, 24, 28, 29, 31, 33], 28)
True
>>> dichotomie([15, 16, 18, 19, 23, 24, 28, 29, 31, 33], 27)
FalseTests :
Affichage :
Console:
3. Le tri fusion (merge sort) :
A copier dans le cahier.
Le tri fusion est un algorithme de tri fondé sur la stratégie du diviser pour régner. Il consiste à découper la liste à trier en sous-listes de plus en plus petites, jusqu’à n’obtenir que des listes d’un seul élément, puis à les fusionner progressivement dans l’ordre croissant.
- Diviser : on coupe la liste en deux parties de taille aussi égale que possible ;
- Régner : on trie récursivement les deux sous-listes obtenues ;
- Combiner : on fusionne les deux listes triées pour obtenir une liste triée complète.
Cet algorithme garantit un temps d’exécution en \(\mathcal{O}\left(n \log(n)\right)\) dans tous les cas, ce qui le rend très fiable même pour de grandes quantités de données.
4. Exercice : fusion!
Compléter la fonction fusion(liste1,liste2), qui prend comme paramètres deux listes triées et qui renvoie une liste triée composée des éléments des deux autres.
Tests :
Affichage :
Console:
5. Exercice : tri fusion
Compléter la fonction tri_par_fusion(liste) en vous appuyant sur la fonction fusion (fusion de deux listes triées) de l'exercice précédent.
Tests :
Affichage :
Console:
6. Exercice :
A faire dans le cahier.
Ce code a permis de générer les 3 images ci-dessous :
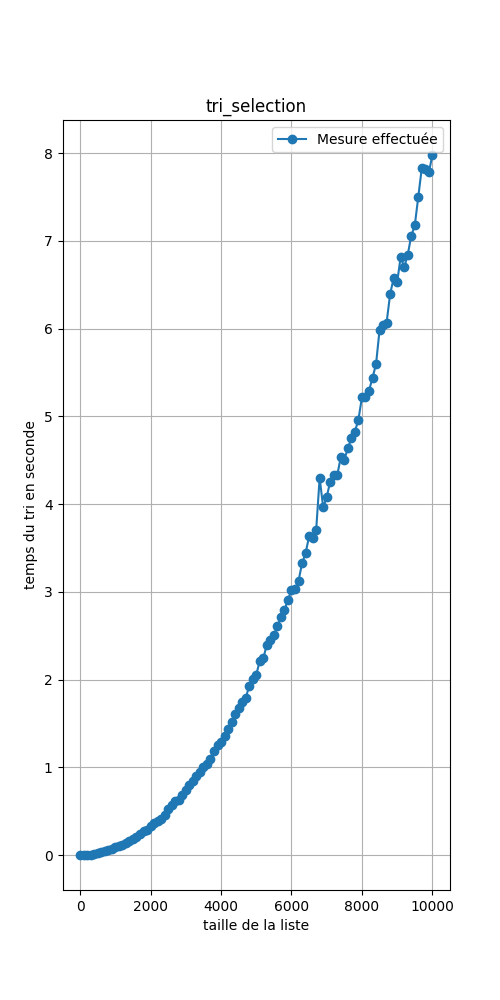
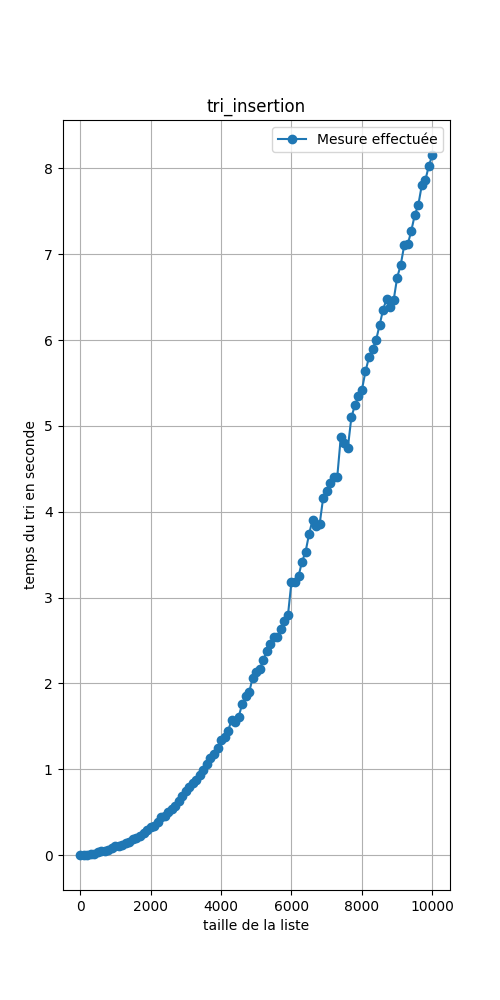
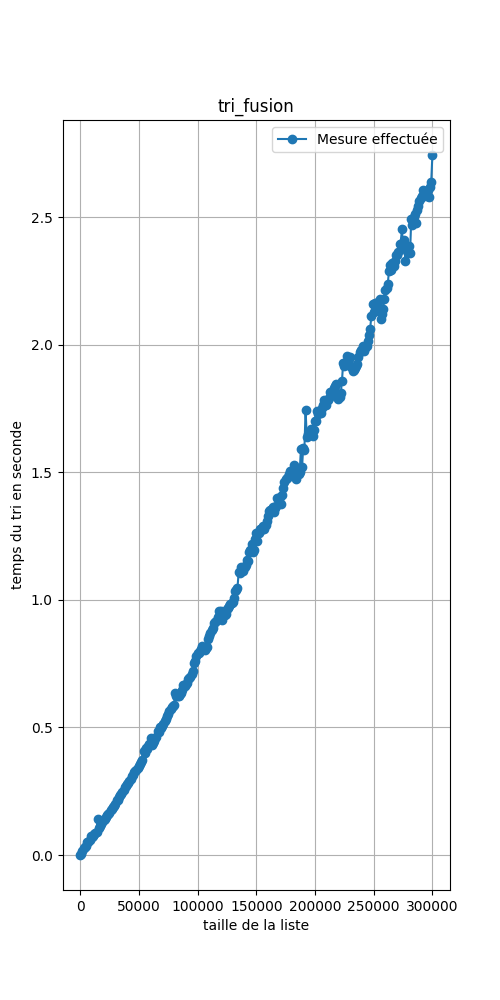
Il peut sembler que les courbes soient similiaires mais :
- Comparer les performances de chaque tri.
- A quelle courbe vue en seconde ressemble les deux premières ci-dessus?
- Quel est l'aspect de la troisième courbe?
- Dans les deux premières courbes:
- Prendre deux points de la courbe dont les abscisses sont à peu près le double l'une de l'autre.
- Calculer une approximation du rapport de ces ordonnées.
- Dans les deux premières courbes:
- Prendre deux points de la courbe dont les abscisses sont à peu près le triple l'une de l'autre.
- Calculer une approximation du rapport de ces ordonnées.
- Dans les deux premières courbes:
- Prendre deux points de la courbe dont les abscisses sont à peu près le quadruple l'une de l'autre.
- Calculer une approximation du rapport de ces ordonnées.
- Dans la troisième courbe:
- Prendre deux points de la courbe dont les abscisses sont à peu près le quadruple l'une de l'autre.
- Calculer une approximation du rapport de ces ordonnées.
7. A retenir !
A copier dans le cahier.
Les tris par insertion et par selection sont de complexités quadratiques en \(\mathcal{O}\left(n^2 \right)\).
Le tri par fusion est de complexité linéarithmique en \(\mathcal{O}\left(n \log(n)\right)\).