Chapitre 6 : Les arbres binaires.
Introduction :
L'idée des arbres binaires est simple : chaque nœud a au maximum deux enfants, un à gauche et un à droite, ce qui permet d'organiser les données de manière structurée pour faciliter certaines opérations comme la recherche ou le tri.

1. Définition :
A copier dans le cahier.
Un arbre binaire est un arbre dont l'arité est égale à deux.
Une fois ceci fixé, nous pouvons ainsi parler d'enfant gauche et d'enfant droit.
2. Exemple :
Dans l'exemple ci-dessus :
- L'enfant gauche de Mary est Margaret.
- Margaret n'a pas d'enfant.
- Elizabeth n'a pas d'enfant gauche.
3. Exercice :
A faire dans le cahier.
Dans cet exercice un arbre composé uniquement d'un seul noeud a une hauteur de 1.
On considère cet arbre binaire :
- Quelle est sa racine?
- Quelle est sa hauteur?
- Quelle est sa taille?
- Combien a-t-il de feuille?
- Qui est l'enfant gauche de l'enfant gauche de l'enfant gauche du parent du parent de Mia?
4. Définition :
Dans un arbre binaire, à partir d'un noeud, on peut considérer son sous-arbre gauche et son sous-arbre droit.
5. Exemple :
6. Arbre localement complet
A copier dans le cahier.
Un arbre est dit localement complet si chaque noeud possède soit 0 soit deux enfants.
7. Exemple :
Cet arbre est localement complet.
8. Arbre complet
A copier dans le cahier.
Un arbre est dit complet s'il est localement complet et que ses noeuds ne comportant pas d'enfant sont au même niveau.
9. Exemple :
Cet arbre est complet.
10. Arbre dégénéré
A copier dans le cahier.
Un arbre est dit dégénéré s'il ne possède qu'une seule feuille.
On peut alors l'associer à une structure linéaire.
11. Exemple :
Cet arbre est dégénéré.
12. Exercice :
A faire dans le cahier.
Représenter l'arbre correspondant au tableau ci-dessous :
| Noeud | Valeur | Enfant gauche | Enfant droit |
|---|---|---|---|
| 1 | René | 2 | 3 |
| 2 | Lilou | 4 | \(\emptyset\) |
| 4 | Léa | \(\emptyset\) | \(\emptyset\) |
| 3 | Julie | \(\emptyset\) | 6 |
| 6 | Chloé | 7 | 8 |
| 7 | Titou | \(\emptyset\) | \(\emptyset\) |
| 8 | Irène | \(\emptyset\) | \(\emptyset\) |
13. Exercice
A faire dans le cahier.
En prenant exemple sur le tableau de l'exercice précédent, faire un tableau correspondant à l'arbre ci-dessous :
14. Une première implémentation dans Python
A copier dans le cahier.
On peut stocker un arbre binaire dans Python à l'aide de liste de liste :
[racine,[sous_arbre_gauche],[sous_arbre_droit]]15. Exercice : Une première implémentation dans Python
Insérer dans Python l'arbre suivant à l'aide de liste de liste.
Une feuille aura ce format : [valeur,None,None]
Tests :
# TestsAffichage :
Console:
16. Exercice : Ajout d’une feuille à gauche (récursif)
Écrire une fonction ajout_feuille_gauche(liste_arbre, valeur) qui prend en paramètre un arbre sous forme de liste et une valeur.
Elle fonctionnera de manière récursive ainsi :
- Si l’enfant gauche de la racine est vide, on place la valeur à cet endroit.
- Sinon, on exécute cette fonction dans le sous-arbre gauche.
Dans le contexte, un arbre est ici stocké dans des listes de listes (format [etiquette, gauche, droite]). Par exemple :
["Olivier",
["Julien", None, None],
["Léa", None, None]]Tests :
Affichage :
Console:
17. Algorithmes de la taille, de la hauteur et du nombre de feuilles d'un arbre.
A copier dans le cahier.
Ces trois algorithmes sont des algorithmes récursifs :
-
Taille d'un arbre :
Fonction taille(arbre) : Si arbre vide : retourne 0 Sinon : retourne 1 +taille(sous-arbre gauche)+ taille(sous-arbre droit) -
Hauteur d'un arbre (cas où un arbre composé seulement de sa racine est de hauteur 1):
Fonction hauteur(arbre) : Si arbre vide : retourne 0 Sinon : retourne 1 +max(hauteur(sous-arbre gauche),hauteur(sous-arbre droit)) -
Nombre de feuilles d'un arbre :
Fonction nombre_feuilles(arbre) : Si arbre vide : retourne 0 Sinon si arbre n'est composé que d'une racine : retourne 1 Sinon : retourne nombre_feuilles(sous-arbre gauche)+ nombre_feuilles(sous-arbre droit)
18. Exercice : Arbres — taille, hauteur, nombre de feuilles
On représente un arbre binaire par une liste de la forme [etiquette, gauche, droite], où gauche et droite sont soit None, soit des sous-arbres au même format.
Écrire en Python les fonctions suivantes :
taille(arbre): renvoie le nombre total de nœuds de l’arbre.hauteur(arbre): renvoie la hauteur de l’arbre (un arbre réduit à un seul nœud a une hauteur égale à 1 ; l’arbre vide a une hauteur de 0).nombre_de_feuilles(arbre): renvoie le nombre de feuilles (nœuds sans enfant) de l’arbre.
Exemple de structure :
["Olivier",
["Julien", None, None],
["Léa", None, None]]Tests :
Affichage :
Console:
19. Parcours en profondeur
A copier dans le cahier.
Parcourir l'arbre en profondeur signifie que l'on explore chaque sous-arbre complètement avant de passer à un autre sous-arbre.
On distingue alors trois cas :
- L'ordre préfixe : on évalue la racine, puis les sous arbres (gauche puis droit).
- L'ordre infixe : on évalue le sous-arbre gauche, puis la racine et enfin le sous-arbre droit.
- L'ordre postfixe : on évalue d'abord les deux sous-arbres (gauche puis droit) et seulement après la racine.
20. Exercice
A faire dans le cahier.
On considère l'arbre suivant:
- Ecrire les valeurs rencontrées en parcourant l'arbre dans l'ordre préfixe.
- Ecrire les valeurs rencontrées en parcourant l'arbre dans l'ordre infixe.
- Ecrire les valeurs rencontrées en parcourant l'arbre dans l'ordre postfixe.
21. Algorithmes parcours en profondeur.
A copier dans le cahier.
Ces trois algorithmes sont des algorithmes récursifs :
-
Parcours préfixe :
Fonction parcours_prefixe(arbre) : Si arbre vide : On ne fait rien Sinon : On évalue la racine On lance parcours_prefixe(sous-arbre gauche) On lance parcours_prefixe(sous-arbre droit) -
Parcours infixe :
Fonction parcours_infixe(arbre) : Si arbre vide : On ne fait rien Sinon : On lance parcours_infixe(sous-arbre gauche) On évalue la racine On lance parcours_infixe(sous-arbre droit) -
Parcours postfixe :
Fonction parcours_postfixe(arbre) : Si arbre vide : On ne fait rien Sinon : On lance parcours_postfixe(sous-arbre gauche) On lance parcours_postfixe(sous-arbre droit) On évalue la racine
22. Exercice : Parcours d'arbre — préfixe, infixe, postfixe (afficher & renvoyer)
On représente un arbre binaire par une liste [etiquette, gauche, droite], où gauche et droite sont soit None, soit des sous-arbres au même format.
lecture_prefixe(arbre): renvoie la liste des valeurs rencontrées en ordre préfixe (racine, gauche, droite).lecture_infixe(arbre): renvoie la liste des valeurs en ordre infixe (gauche, racine, droite).lecture_postfixe(arbre): renvoie la liste des valeurs en ordre postfixe (gauche, droite, racine).
Tests :
Affichage :
Console:
23. Implementation à l'aide d'une classe :
On peut implémenter un arbre dans Python avec une classe de différentes façons.
Afin de faciliter les différentes corrections, nous utiliserons la même qui est celle-ci:
class ArbreBinaire:
def __init__(self, valeur):
self.valeur = valeur
self.gauche = None
self.droit = None
def ajout_gauche(self, valeur):
self.gauche = ArbreBinaire(valeur)
def ajout_droit(self, valeur):
self.droit = ArbreBinaire(valeur)
def suppr_gauche(self):
self.gauche = None
def suppr_droit(self):
self.droit = None24. Exercice : Construire l'arbre donné (classe fournie)
Compléter le code pour créer l’instance arbre et tous ses descendants en utilisant ajout_gauche / ajout_droit.
Tests :
Affichage :
Console:
25. Exercice : Taille, hauteur et nombre de feuilles (classe ArbreBinaire)
On représente un arbre binaire avec la classe ArbreBinaire (valeur, gauche, droit). Écrire les fonctions suivantes :
taille(arbre): renvoie le nombre total de nœuds (0 si l’arbre est vide) ;hauteur(arbre): renvoie la hauteur (0 si vide, 1 si un seul nœud) ;nombre_feuilles(arbre): renvoie le nombre de feuilles (nœuds sans enfant).
Tests :
Affichage :
Console:
26. Exercice : Parcours d'arbre — préfixe, infixe, postfixe (classe ArbreBinaire)
On représente un arbre binaire avec la classe ArbreBinaire (valeur, gauche, droit). Écrire des fonctions qui renvoient la liste des valeurs rencontrées :
lecture_prefixe(racine): ordre préfixe (racine, gauche, droite) ;lecture_infixe(racine): ordre infixe (gauche, racine, droite) ;lecture_postfixe(racine): ordre postfixe (gauche, droite, racine).
Tests :
Affichage :
Console:
27. Parcours de l'arbre en largeur (aussi appelé "en largeur d'abord") :
Nous avons vu que nous pouvons parcourir un arbre en profondeur. Nous pouvons aussi le parcourir en largeur d'abord.
Il suffit d'évaluer les valeurs de chaque noeud niveau par niveau.
28. Exercice
A faire dans le cahier.
On considère l'arbre suivant:
Dans votre cahier, écrire les valeurs des noeuds rencontrés par un parcours en largeur.
29. Algorithme du parcours en largeur d'un arbre:
A copier dans le cahier.
fonction parcours_largeur(arbre):
si arbre vide:
On ne fait rien
sinon :
on place l'arbre dans une file.
tant que la file n'est pas vide:
on sort un element de la file
on affiche la valeur de la racine
on place le sous-arbre gauche dans la file s'il n'est pas vide
on place le sous-arbre droit dans la file s'il n'est pas vide30. Exercice : Parcours en largeur (classe ArbreBinaire + File)
On représente un arbre binaire avec la classe ArbreBinaire (valeur, gauche, droit).
Écrire une fonction parcours_largeur(arbre) qui renvoie la liste des valeurs rencontrées lors du parcours en largeur de l’arbre (niveau par niveau de gauche à droite).
Pour cela, on utilisera une classe File permettant de gérer une file FIFO avec les méthodes :
enfiler(x): ajoute un élément en fin de file ;defiler(): retire et renvoie le premier élément de la file ;est_vide(): renvoie True si la file est vide.
Exemple :
# 'A'
# / \
# 'B' 'C'
# / \ \
# 'D' 'E' 'F'
# Le parcours en largeur renvoie : ['A', 'B', 'C', 'D', 'E', 'F']Tests :
Affichage :
Console:
31. Calculs à l'aide d'un arbre :
Un arbre permet de stocker un calcul tout en précisant les priorités opératoires à effectuer.
32. Exemple :
On considère l'arbre suivant:
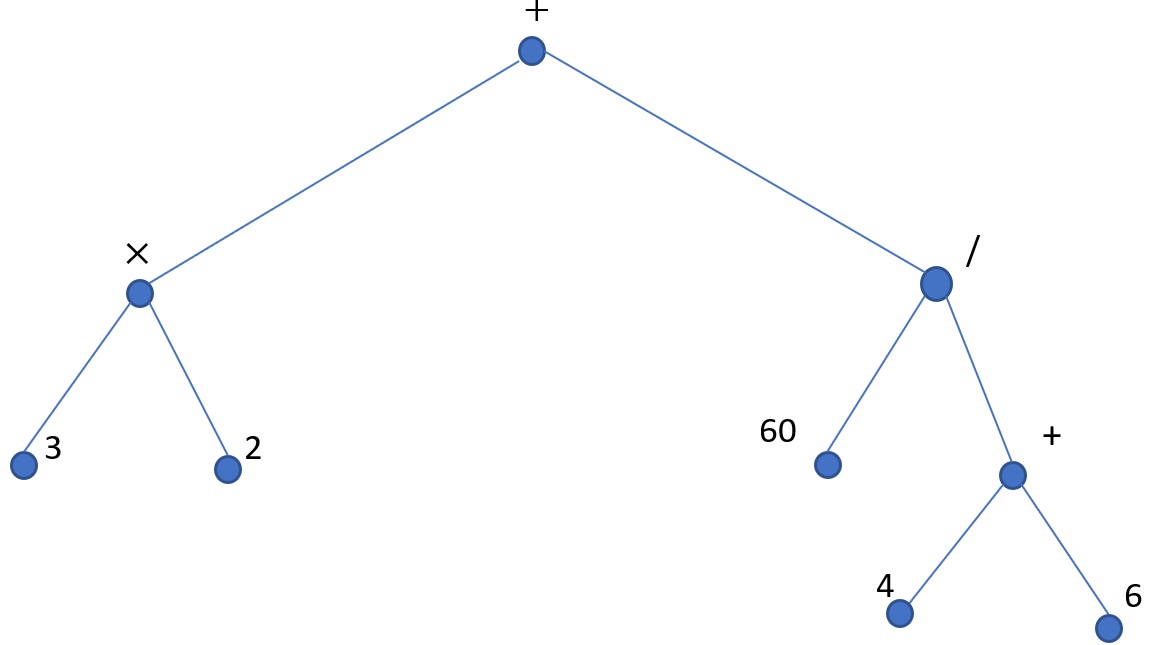
Il permet de stocker le calcul suivant : \( 3 \times 2 + \frac{60}{4+6}\)
33. Exercice :
A faire dans le cahier
On considère l'arbre de l'exemple précédent.
- Ecrire les valeurs rencontrées en parcourant l'arbre dans l'ordre préfixe.
- Ecrire les valeurs rencontrées en parcourant l'arbre dans l'ordre infixe.
- Ecrire les valeurs rencontrées en parcourant l'arbre dans l'ordre postfixe.
34. Ecriture en ligne d'un parcours postfixé ou préfixé d'un arbre contenant une expression mathématique :
Certains langages de programmation ou même de calculatrice utilisent de telles notations pour calculer.
35. Exemples :
-
Par exemple le langage scheme utilise une notation en ligne d'un parcours préfixe d'un arbre contenant une expression mathématique.
On peut y trouver de telles notations : print(+ (- 3 2) 5)
-
La calculatrice HP utilise une notation postfixe
https://fr.wikipedia.org/wiki/HP-25
36. Exercice : Évaluer une expression dans un arbre binaire
On représente une expression mathématique sous forme d’arbre binaire à l’aide de la classe ArbreBinaire. Chaque nœud contient soit un opérateur (+, -, *, /), soit un entier.
Programmer une fonction Python evaluer qui prend comme paramètre un objet ArbreBinaire contenant une expression mathématique et qui renvoie le résultat numérique.
Tests :
Affichage :
Console:
37. Exercice : (sujet 35 - 2025)
Nous avons l’habitude de noter les expressions arithmétiques avec des parenthèses comme par exemple : \((2 + 3) \times 5\).
Il existe une autre notation utilisée par certaines calculatrices, appelée notation postfixe, qui n’utilise pas de parenthèses. L’expression arithmétique précédente est alors obtenue en saisissant successivement 2, puis 3, puis l’opérateur +, puis 5, et enfin l’opérateur *. On modélise cette saisie par le tableau [2, 3, '+', 5, '*'].
Autre exemple, la notation postfixe de \(3 \times 2 + 5\) est modélisée par le tableau :
[3, 2, '*', 5, '+']D’une manière plus générale, la valeur associée à une expression arithmétique en notation postfixe est déterminée à l’aide d’une pile en parcourant l’expression de gauche à droite :
- si l’élément parcouru est un nombre, on le place au sommet de la pile,
- si l’élément parcouru est un opérateur, on récupère les deux éléments situés au sommet de la pile et on leur applique l’opérateur, puis on place le résultat au sommet de la pile,
- à la fin du parcours, il reste alors un seul élément dans la pile qui est le résultat de l’expression arithmétique.
Dans cet exercice, on se limitera aux opérations * et +.
Complète la fonction eval_expression qui reçoit en paramètre une liste python représentant la notation postfixe d’une expression arithmétique et qui renvoie sa valeur.
⭐ Exemple :
>>> eval_expression([2, 3, '+', 5, '*'])
25Tests :
Affichage :
Console:
38. Exercice (sujet 30 - 2025)
Une expression arithmétique ne comportant que les quatre opérations \(+\), \(-\), \( \times \) , \( \div \) peut être représentée sous forme d’arbre binaire. Les nœuds internes sont des opérateurs et les feuilles sont des nombres. Dans un tel arbre, la disposition des nœuds joue le rôle des parenthèses que nous connaissons bien.
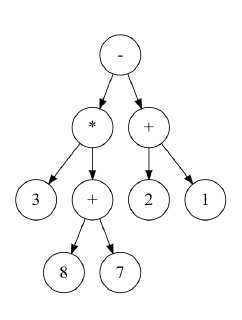
En parcourant en profondeur infixe l’arbre binaire ci-dessus, on retrouve l’expression notée habituellement :
\((3 \times (8 + 7)) – (2 + 1)\)
La classe Expr ci-après permet d’implémenter une structure d’arbre binaire pour représenter de telles expressions.
Compléter la méthode récursive infixe qui renvoie une chaîne de caractères contenant des parenthèses représentant l’expression arithmétique sur laquelle on l’applique.
Tests :
Affichage :
Console:
39. Exercice : (sujet 47 - 2025)
Un arbre binaire de caractères est stocké sous la forme d’un dictionnaire où les clés sont les caractères des nœuds de l’arbre et les valeurs, pour chaque clé, la liste des caractères des fils gauche et droit du nœud.
Par exemple, l’arbre
est stocké dans
a = {'F':['B','G'], 'B':['A','D'], 'A':['',''], 'D':['C','E'],'C':['',''], 'E':['',''], 'G':['','I'], 'I':['','H'], 'H':['','']}Écrire une fonction récursive taille prenant en paramètres un arbre binaire arbre
sous la forme d’un dictionnaire et un caractère lettre qui est la valeur du sommet de
l’arbre, et qui renvoie la taille de l’arbre, à savoir le nombre total de nœud.
On observe que, par exemple, arbre[lettre][0], respectivement
arbre[lettre][1], permet d’atteindre la clé du sous-arbre gauche, respectivement
droit, de l’arbre arbre de sommet lettre.
Exemple :
>>> taille(a, 'F')
9Tests :
Affichage :
Console:
40. Exercice :
Il est moins usuel mais nous pouvons programmer un parcours préfixé en itératif à l'aide de l'algorithme suivant :
fonction parcours_prefixe_iteratif(arbre):
créer une pile p
insérer l'arbre dans la pile
tant que la pile p n'est pas vide
depiler un element de la pile que l'on nommera element
traiter la racine de cet element en l'affichant par exemple
si le sous-arbre droit n'est pas vide :
on empile dans p le sous-arbre droit
si le sous arbre gauche n'est pas vide :
on empile dans p le sous-arbre gaucheCoder ceci en python à l'aide des classes ArbreBinaire et Pile. On pourra utiliser un arbre des exercices précédents.
Tests :
Affichage :
Console:
41. Exercice : (sujet 11 - 2025)
Un arbre binaire est soit vide, représenté en Python par la valeur None, soit un nœud représenté par un triplet (g, x, d) où x est l’étiquette du nœud et g et d sont les sous-arbres gauche et droit.
On souhaite écrire une fonction parcours_largeur qui prend en paramètre un arbre binaire et qui renvoie la liste des étiquettes des nœuds de l’arbre parcourus en largeur.
Exemples :
>>> arbre = ( ( (None, 1, None), 2, (None, 3, None) ),
... 4,
... ( (None, 5, None), 6, (None, 7, None) ) )
>>> parcours_largeur(arbre)
[4, 2, 6, 1, 3, 5, 7]Tests :
Affichage :
Console: