Chapitre 10 : Tri par insertion.

Introduction :

Le tri par insertion est un autre algorithme de tri qui fonctionne en construisant une liste triée un élément à la fois.

Contrairement au tri par sélection, où on cherche le plus petit élément à chaque étape, le tri par insertion prend chaque élément de la liste non triée et l'insère à sa place correcte dans la partie déjà triée. Ce processus est répété pour tous les éléments.

Le tri par insertion est souvent plus efficace que le tri par sélection pour les petites listes ou les listes déjà partiellement triées, mais il a également une complexité en temps de O(n2)O(n2) dans le pire des cas.

1. Tri par insertion .

A copier dans le cahier.

Le tri par insertion est un algorithme de tri simple qui construit une liste triée un élément à la fois en insérant chaque élément à sa place appropriée dans la partie triée de la liste.

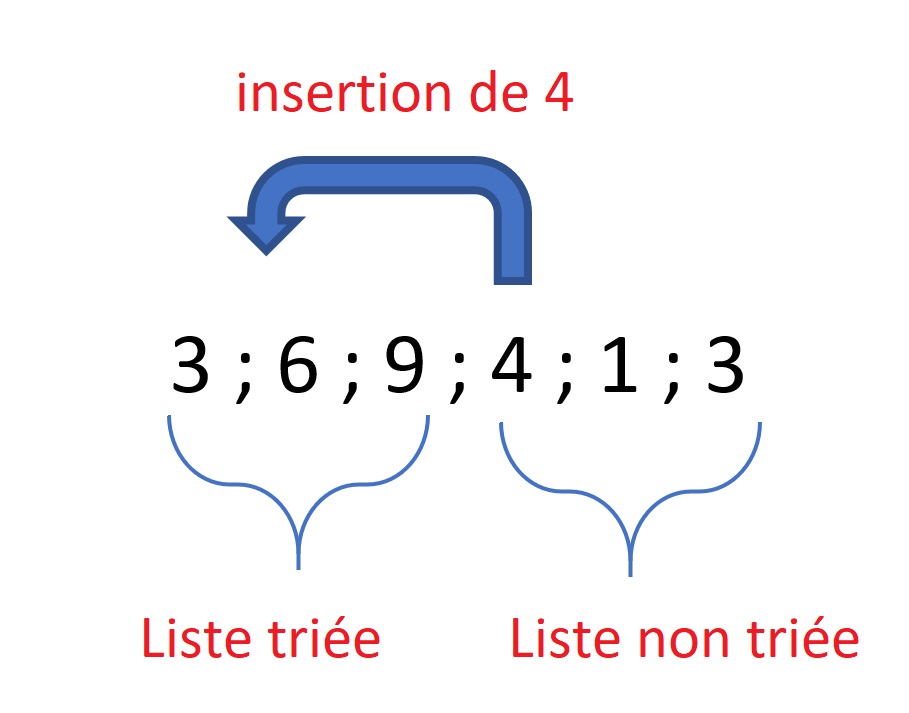
L'algorithme de tri par insertion fonctionne comme suit :

Commencer avec le deuxième élément (l'élément à l'index 1) et le comparer avec le premier élément. Si le deuxième élément est plus petit, les échanger.
Continuer à déplacer l'élément comparé vers la gauche jusqu'à ce qu'il atteigne sa position appropriée parmi les éléments triés précédents.
Répéter les étapes 1 et 2 pour tous les éléments suivants dans la liste non triée.

2. Exercice :

A faire dans le cahier.

A la main :

Trier la liste [42, 17, 9, 87, 23, 56, 34, 71, 5, 91] en mettant une ligne par étape avec un algorithme de tri par insertion.

3. Pseudo-code du tri par insertion

À copier dans le cahier.

Pseudo-code

Algorithme TRI_INSERTION(tab)
    n ← longueur(tab)
    Pour i allant de 1 à n-1 faire
        clé ← tab[i]
        j ← i - 1
        Tant que j ≥ 0 et tab[j] > clé faire
            tab[j+1] ← tab[j]
            j ← j - 1
        tab[j+1] ← clé
    Renvoyer tab

4. Exercice

Compléter la fonction tri_insertion ci-dessous pour trier une liste en utilisant l’algorithme du tri par insertion. La fonction modifie la liste sur place.

def tri_insertion(tab): ... import random liste = [random.randint(1, 1000) for _ in range(20)] print(f"liste initiale : {liste}") tri_insertion(liste) print(f"liste triée : {liste}")

Tests :

# Tests

Affichage :

Console:

>>>

5. Exercice :

À faire dans le cahier.

On veut prouver la correction de l’algorithme de tri par insertion à l’aide d’un invariant de boucle.

Rappel du pseudo-code :

Algorithme TRI_INSERTION(tab)
    n ← longueur(tab)
    Pour i allant de 1 à n-1 faire
        clé ← tab[i]
        j ← i - 1
        Tant que j ≥ 0 et tab[j] > clé faire
            tab[j+1] ← tab[j]
            j ← j - 1
        tab[j+1] ← clé
    Renvoyer tab

Propose un invariant de boucle pour la boucle externe (celle sur i).
Montre que l’invariant est vrai au début (initialisation).
Montre que l’invariant est conservé après une itération (conservation).
Explique pourquoi, à la fin de la boucle, l’invariant permet de conclure que le tableau est trié.

6. Complexité du tri par insertion

Principe du tri par insertion

Le tri par insertion consiste à construire progressivement une partie triée du tableau, en insérant chaque nouvel élément à la bonne place.

Nombre de comparaisons

Soit un tableau de taille \( n \).

Dans le pire des cas (lorsque le tableau est trié dans l’ordre décroissant), chaque nouvel élément doit être comparé à tous ceux qui le précèdent pour être inséré à la bonne place.

Plus précisément :

le deuxième élément est comparé avec le premier : 1 comparaison ;
le troisième élément est comparé avec les deux premiers : 2 comparaisons ;
le quatrième élément est comparé avec les trois premiers : 3 comparaisons ;
et ainsi de suite jusqu’au dernier élément, comparé \( n - 1 \) fois.

Le nombre total de comparaisons est donc :

\( 1 + 2 + \dots + (n - 1) \)

Calcul de la somme

Cette somme vaut :

\( 1 + 2 + \dots + (n - 1) = \frac{n(n - 1)}{2} \)

Complexité temporelle

Le terme dominant de \( \frac{n(n - 1)}{2} \) est \( n^2 \).

La complexité du tri par insertion dans le pire des cas est donc : \( \mathcal{O}(n^2) \).

Cas particulier favorable

Si le tableau est déjà presque trié, le nombre de comparaisons est faible.
Dans le meilleur des cas (tableau déjà trié), la complexité est \( \mathcal{O}(n) \).

Le tri par insertion est donc plus efficace que le tri par sélection sur des tableaux presque triés.